Question

【题目】自行车因其便捷环保深受人们喜爱，成为日常短途代步与健身运动首选．如图1是某品牌自行车的实物图，图2是它的简化示意图．经测量，车轮的直径为66cm，车座B到地面的距离BE为90cm，中轴轴心C到地面的距离CF为33cm，车架中立管BC的长为60cm，后轮切地面L于点D．（参考数据：sin72≈0.95，cos18°≈0.95，tan43.5°≈0.9 5）

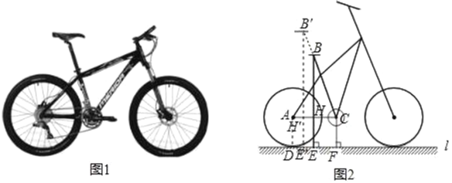
（1）求∠ACB的大小（精确到1°）

（2）如果希望车座B到地面的距离B'E′为96.8cm，车架中立管BC拉长的长度BB′应是多少？（结果取整数）

Answer 1

【答案】（1）∠ACB＝72°；（2）车架中立管BC拉长的长度BB'应是7cm．

【解析】

（1）根据矩形的判定可得：四边形ADFC是矩形，从而求出BH，利用sin∠BCH＝，即可求出∠BCH；

（2）设B'E'与AC交于点H'，根据平行可证：B'H'∥BH，从而列出比例式即可求出B'C，从而求出BB′的长度.

（1）∵AD⊥l，CF⊥l，HE⊥l

∴AD∥CF∥HE，

∵AD＝33cm，CF＝33cm，

∴AD＝CF，

∴四边形ADFC是平行四边形，

∵∠ADF＝90°，

∴四边形ADFC是矩形，

∴HE＝AD＝33cm，

∵BE＝90cm，

∴BH＝57cm，

在Rt△HCB中，sin∠BCH＝＝＝＝0.95，

∴∠ACB＝72°．

（2）如图所示，B'E'＝96.8cm，设B'E'与AC交于点H'，则有B'H'∥BH，

∴△B'H'C∽△BHC，

∴＝．

即＝，

∴B'C＝67cm．

故BB'＝B'C﹣BC＝67﹣60＝7（cm）．

∴车架中立管BC拉长的长度BB'应是7cm．