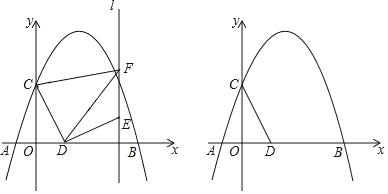
题目内容
【题目】已知直角△ABC,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF连接EF

(1)如图1,求证:∠BED=∠AFD;
(2)求证:BE2+CF2=EF2;
(3)如图2,当∠ABC=45°,若BE=12,CF=5,求△DEF的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用四边形内角和得出∠AED+∠AFD=180°,再根据补角的性质即可得;
(2)延长ED至点P,使ED=DP,构造全等三角形,利用全等三角形的性质得到直角三角形,由勾股定理及等量代换可得;
(3)由(2)结论求EF长,再通过全等证明DE=DF,由面积公式求解.
解:(1)∵DE⊥DF,
∴∠EDF=90°,
∵∠BAC=90°,
∴∠AED+∠AFD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠AFD;
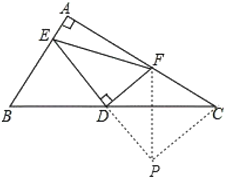
(2)如图,
延长ED至点P,使ED=DP,连接CP,EP,
∵FD⊥EP,
∴FD为EP的垂直平分线,
∴EF=FP,
∵ED=DP, ∠EDB=∠CDP,BD=CD,
∴△EDB≌PDC,
∴EB=CP, ∠B=∠DCP,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠DCP+∠ACB=90°,
即∠ACP=90°,
由勾股定理得,CP2+CF2=FP2,
∴BE2+CF2=EF2;
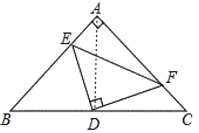
(3)如图,∵BE2+CF2=EF2
∴52+122=EF2,
∴EF=13,
∵△ABC是等腰直角三角形,BD=CD,
∴AD⊥BC, ∴∠ADC=90°, ∠BAD=∠B=∠C=45°,
∵∠EDF=90°
∴∠ADE=∠CDF,
∴△ADE≌CDF,
∴DE =DF=![]() ,
,
∴S△DEF=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.

(1)我们先从特殊的倍角三角形入手研究.请你结合图形填空:
三三角形角形 | 角的已知量 |
|
|
图2 | ∠A=2∠B=90° | ||
图3 | ∠A=2∠B=60° |
(2)如图4,对于一般的倍角△ABC,若∠CAB=2∠CBA,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图4给出的辅助线提示加以证明;
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长.(直接写出结论即可)