题目内容
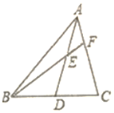
【题目】如图,菱形ABCD的较短对角线BD为4,∠ADB=60°,E、F分别在AD,CD上,且∠EBF=60°.
(1)求证:△ABE≌△DBF;
(2)判断△BEF的形状,并说明理由.

【答案】(1)证明见解析;(2)结论:△BEF是等边三角形.理由见解析.
【解析】
(1)首先证明△ABD,△BDC都是等边三角形,再证明∠ABE=∠DBF,即可解决问题;
(2)根据全等三角形的性质可知BE=BF,结合∠EBF=60°即可证明;
(1)证明:∵四边形ABCD是菱形,
∴AD=AB,
∵∠ADB=60°,
∴△ADB是等边三角形,△BDC是等边三角形,
∴AB=BD,∠ABD=∠A=∠BDC=60°,
∵∠ABD=∠EBF=60°,
∴∠ABE=∠DBF,
在△ABE和△DBF中,
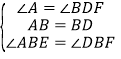 ,
,
∴△ABE≌△DBF.
(2)结论:△BEF是等边三角形.
理由:∵△ABE≌△DBF,
∴BE=BF,∵∠EBF=60°,
∴△EBF是等边三角形.

练习册系列答案
相关题目