题目内容
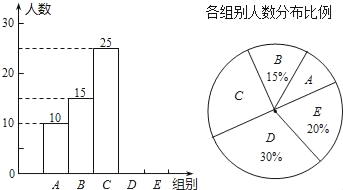
【题目】重庆八中宏帆中学某年级为了选拔参加“全国汉字听写大赛”重庆赛区比赛的队员,特在年级举行全体学生的“汉字听写”比赛,首轮每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如图的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)已知该年级共有1500名学生,如果听写正确的字的个数不少于24个则进入第二轮的比赛,请你估计本次听写比赛顺利进入第二轮的学生人数;
(3)第二轮比赛过后,为了更有针对性地应对本次大赛,该年级决定从没有担任班主任的5个语文老师(其中3个男老师2个女老师)中随机抽取两个老师对胜出的学生进行培训、辅导.请用树状图或列表法求出抽取的两个老师恰好都是男老师的概率.
【答案】(1)30;20;条形统计图见解析;(2)750人;(3)![]()
【解析】
(1)根据B组的人数与所占百分比得到调查的学生总数,再用调查的学生总数乘以D,E组所占百分比即可;
(2)用学校总人数乘以D,E组所占百分比即可得解;
(3)根据题意画出树状图,得到所有等可能的结果数与抽取的两个老师恰好都是男老师的结果数,再利用概率公式求解即可.
解:(1)调查的学生总数为15÷15%=100(人),
则m=100×30%=30,n=100×20%=20,
如图,

(2)1500×(30%+20%)=750,
所以估计本次听写比赛顺利进入第二轮的学生人数为750人;
(3)画出树状图为:

共有20种等可能的结果数,其中抽取的两个老师恰好都是男老师的结果数为6,
所以抽取的两个老师恰好都是男老师的概率=![]() =
=![]() .
.

【题目】如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是 ( )

A. BC=EFB. ∠A=∠EDFC. AB∥DED. ∠BCA=∠F
【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?




