题目内容
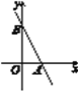
【题目】(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

【答案】(1)∠A+∠B+∠C+∠D+∠E=180°;(2)成立;(3)成立;(4)∠A+∠B+∠C+∠D+∠E=180°.
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠D=∠1,在△BCE中,利用三角形的内角和列式计算即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;
(4)延长CE与AD相交,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠E=∠2,然后利用三角形的内角和定理列式即可得解.
(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图,由三角形的外角性质,∠A+∠D=∠1,
∵∠1+∠DBE+∠C+∠E=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°;
(3)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图,延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.

 阅读快车系列答案
阅读快车系列答案【题目】某商场计划购进冰箱、彩电进行销售,已知冰箱的进货单价比彩电的进货单价多400元,若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等.该商场冰箱、彩电的售货单价如下表:
冰箱 | 彩电 | |
售价(元/台) | 2500 | 2000 |
(1)分别求出冰箱、彩电的进货单价.
(2)为了满足市场需求,商场决定用不超过90 000元的资金采购冰箱、彩电共50台。若该商场将购进的冰箱、彩电共50台全部售出,获得利润为w元,为了使商场的利润最大,该商场该如何购进冰箱、彩电,最大利润是多少?
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
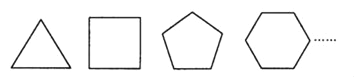
(1)请根据下列图形,填写表中空格:
正多边形边数 | 3 | 4 | 5 | 6 | … |
正多边形每个内角的度数 | … |
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
统计发现两班总分相等,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.