题目内容
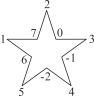
【题目】如图，将－2，－1，0，1，2，3，4，5，6，7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数)，将每一条线上的4个数相加，共得5个数，设为a1，a2，a3，a4，a5.
(1)求
(a1＋a2＋a3＋a4＋a5)的值；
(2)交换其中任何两位数的位置后，(a1＋a2＋a3＋a4＋a5)的值是否改变？并说明理由．
【答案】（1）25（2）等于
【解析】
（1）分别算出每一行上的四个数的和，即可得到结果．
（2）由①得，无论位置如何变换，这10个数都要用两遍，那么和不会变化．
解：(1)a1＋a2＋a3＋a4＋a5.
＝2×(－1－2＋0＋1＋2＋3＋4＋5＋6＋7).
＝50.
(2)交换其中任何两数的位置后，a1＋a2＋a3＋a4＋a5的值不变，仍为50.
理由：无论怎样改变位置，其中的每个数都用了两次，即a1＋a2＋a3＋a4＋a5.
＝2×(－1－2＋0＋1＋2＋3＋4＋5＋6＋7).
＝2×25.
＝50.
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
