题目内容
【题目】(1)、菱形![]() 的边长1,面积为
的边长1,面积为![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
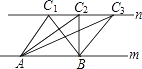
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

【答案】(1)B;(2)15°.
【解析】
试题分析:(1)在菱形ABCD中,设AO=x,BO=y,根据菱形的性质得出: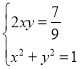 求出x、y的值即可求出AC+BD的值.
求出x、y的值即可求出AC+BD的值.
(2)过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为![]() ,即菱形的四条边为
,即菱形的四条边为![]() ,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为
,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为![]() ,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
(1)在菱形ABCD中,设AO=x,BO=y,
根据菱形的性质得出: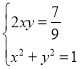 解得
解得![]()
∴AC+BD=2(x+y)=2×![]() =
=![]() .
.
故选B.
(2)过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD=![]() ,
,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD=![]() ,
,
又BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG∠BDC=90°45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=![]() ,
,
又DF=![]() ,
,
在Rt△DFG中,由DG=![]() DF,
DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC∠DBE=45°30°=15°.