题目内容
【题目】如图,在等腰直角三角形![]() 和
和![]() 中,点
中,点![]() 为它们的直角顶点,当
为它们的直角顶点,当![]() 与
与![]() 有重叠部分时:
有重叠部分时:
(1)①连接![]() ,如图1,求证:
,如图1,求证: ![]() ;
;
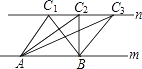
②连接![]() ,如图2,求证:
,如图2,求证: ![]() ;
;
(2)当![]() 与
与![]() 无重叠部分时:连接
无重叠部分时:连接![]() ,如图3,当
,如图3,当![]() ,
, ![]() 时,计算四边形
时,计算四边形![]() 面积的最大值,并说明理由.
面积的最大值,并说明理由.



【答案】(1) ①见解析;②见解析;(2)![]()
【解析】试题分析:(1)①利用同角的余角相等证出∠ACD=∠BCE,然后利用“SAS”证明△ACD≌△BCE即可得出结论;
②因为△ACE与△CDB的一条边AC=BC,所以要证两个三角形的面积相等只要证明AC和BC边上的高相等即可,过点E作EF⊥AC,过点D作DH⊥BC,通过证明△CEF≌△CDH即可得出结论;
(2)设△BCD的BC边上的高为h,同(1)②的方法可得S△ACE=S△BCD,所以S四边形ABDE=S△ABC+S△CDE+S△ACE+S△BCD=![]() +5h,而h≤CD,故当h=CD=2时S四边形ABDE最大,代入h=2求出最大值即可.
+5h,而h≤CD,故当h=CD=2时S四边形ABDE最大,代入h=2求出最大值即可.
试题解析:
解:(1)①∵∠ACD+∠BCD=90°,∠BCE+∠BCD=90°,
∴∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②如图:作EF⊥AC交AC的延长线于点F,作DH⊥BC于点H,
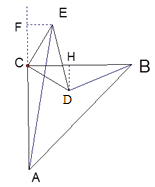
∵∠FCE+∠ECH=90°,∠HCD+∠ECH=90°,
∴∠FCE=∠HCD,
∵∠EFC=∠DHC=90°,CE=CD,
∴△CEF≌△CDH(AAS),
∴EF=DH,
∵S△ACE=![]() AC·EF,S△CDB=
AC·EF,S△CDB=![]() BC·DH,AC=BC,
BC·DH,AC=BC,
∴S△ACE=S△CDB;
(2)设△BCD的BC边上的高为h,
同(1)②的方法可得S△ACE=S△BCD,
∴S四边形ABDE=S△ABC+S△CDE+S△ACE+S△BCD=![]() ×52+
×52+![]() ×22+2 S△BCD =
×22+2 S△BCD =![]() +5h,
+5h,
∵h≤CD,
∴当h=CD=2时S四边形ABDE最大,
∴四边形ABDE的面积最大值为![]() +5×2=
+5×2=![]() .
.