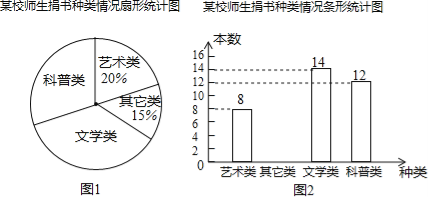
题目内容
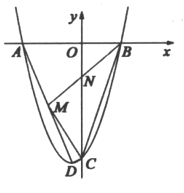
【题目】如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.
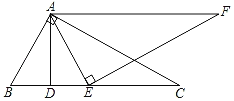
(1)填空:AC=_____;∠F=______.
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是____.
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围_____.
【答案】(1)2![]() ,30°;(2)见解析;(3)
,30°;(2)见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)利用∠B的正切值可求出AC的长;根据直角三角形两锐角互余的关系即可求出∠F的度数;
(2)根据垂直平分线的性质可得AB=AE,利用ASA即可证明△ABC≌△EAF;
(3)由∠EAF=60°,∠AEF=90°可得EF=![]() AE,进而可得AE⊥BC时△EAF面积最小,利用∠B的正弦可求出AE的值,进而可求出△EAF的面积;
AE,进而可得AE⊥BC时△EAF面积最小,利用∠B的正弦可求出AE的值,进而可求出△EAF的面积;
(4)如图,当△EAF的内心在AC边上时,设内心为N,根据内心的定义可知∠EAC=30°,可求出∠BAE=60°,可证明△BAE是等边三角形,可求出AE=AB=2,由(1)可知AC=2![]() ,即可得出AE的取值范围.
,即可得出AE的取值范围.
(1)∵∠BAC=90°,∠B=60°,AB=2,tanB=![]() ,
,
∴AC=ABtanB=2tan60°=2![]() ;
;
∵AE⊥EF,
∴∠AEF=90°,
∵∠EAF=∠B=60°,
∴∠F=90°﹣∠EAF=90°﹣60°=30°.
故答案为:2![]() ,30°;
,30°;
(2)当BD=DE时,
∵AD⊥BC于D,
∴AB=AE,
∵∠AEF=90°,∠BAC=90°,
∴∠AEF=∠BAC,
在△ABC和△EAF中,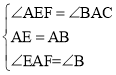 ,
,
∴△ABC≌△EAF(ASA);
(3)∵∠AEF=90°,∠EAF=60°,tan∠EAF=![]() ,
,
∴EF=AEtan∠EAF=AEtan60°=![]() AE,
AE,
∴S△EAF=![]() AEEF=
AEEF=![]() AE×
AE×![]() AE=
AE=![]() AE2,
AE2,
当AE⊥BC时,AE最短,S△EAF最小,此时∠AEB=90°,sinB=![]() ,
,
∴AE=ABsinB=2sin60°=2×![]() =
=![]() ,
,
S△EAF=![]() AE2=
AE2=![]() ×3=
×3=![]() ,
,
∴△EAF面积的最小值是![]() ,
,
故答案为:![]() ;
;
(4)设△EAF的内心为N,
∵![]() ∠AEF=45°,
∠AEF=45°,![]() ∠B=30°,E为BC上的一点,不与B、C重合,
∠B=30°,E为BC上的一点,不与B、C重合,
∴EN与AC一定有交点,
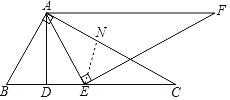
如图:当△EAF内心恰好落在AC上时,连接EN,
∵N是△EAF的内心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=![]() ∠AEF=
∠AEF=![]() ×60°=30°,
×60°=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC﹣∠EAC=90°﹣30°=60°,
∵∠B=60°,
∴△ABE是等边三角形,
∴AE=AB=2,
∵E为BC上的一点,不与B、C重合,由(1)可知AC=2![]() ,
,
∴当△EAF的内心在△ABC的外部时,![]() .
.
故答案为:![]() .
.