题目内容

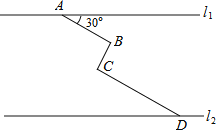
【题目】如图，在同一平面内，两条平行高速公路l1和l2间有一条“Z”型道路连通，其中AB段与高速公路l1成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速公路间的距离（结果保留根号）．

【答案】km

【解析】

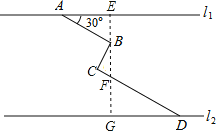
过B点作BE⊥l1，交l1于E，CD于F，l2于G．在Rt△ABE中，根据三角函数求得BE，在Rt△BCF中，根据三角函数求得BF，在Rt△DFG中，根据三角函数求得FG，再根据EG=BE+BF+FG即可求解．

过B点作BE⊥l1，交l1于E，CD于F，l2于G．

在Rt△ABE中，BE=ABsin30°=20×=10km，

在Rt△BCF中，BF=BC÷cos30°=10÷km，

CF=BFsin30°=km，

DF=CD﹣CF=（30﹣）km，

在Rt△DFG中，FG=DFsin30°=（30﹣）×=（15﹣）km，

∴EG=BE+BF+FG=（25+5）km．

故两高速公路间的距离为（25+5）km．

练习册系列答案
相关题目

【题目】（1）已知：如图1，四边形ABCD内接于⊙O，延长BC至E．求证：∠A+∠BCD=180°，∠DCE=∠A．

（2）依已知条件和（1）中的结论：

①如图2，若点C在⊙O外，且A、C两点分别在直线BD的两侧．试确定∠A+∠BCD与180°的大小关系；

②如图3，若点C在⊙O内，且A、C两点分别在直线BD的两侧．试确定∠A+∠BCD与180°的大小关系．

【题目】如图，已知方格纸中的每个小方格都是相同的正方形（边长为1），方格纸上有一个角∠AOB，A，O，B均为格点，请回答问题并只用无刻度直尺和铅笔，完成下列作图并简要说明画法：

（1）OA＝_____；

（2）作出∠AOB的平分线并在其上标出一个点Q，使OQ＝．

【题目】一段抛物线C：y＝﹣x2+3x+m（0≤x≤3）与直线y＝x+1有唯一公共点，若m为整数，则符合条件的所有m的值的和为_____．

【题目】一次函数y＝kx+b的图象与反比例函数y＝的图象相交于A（﹣1，m），B（n，﹣1）两点．

（1）求出这个一次函数的表达式．

（2）求△OAB的面积．

（3）直接写出使一次函数值大于反比例函数值的x的取值范围．

【题目】某市政部门为了保护生态环境，计划购买A，B两种型号的环保设备．已知购买一套A型设备和三套B型设备共需230万元，购买三套A型设备和两套B型设备共需340万元．

（1）求A型设备和B型设备的单价各是多少万元；

（2）根据需要市政部门采购A型和B型设备共50套，预算资金不超过3000万元，问最多可购买A型设备多少套？

【题目】如图，An系列矩形纸张的规格特征是：①各矩形纸张都相似；②A1纸对裁后可以得到两张A2纸，A2纸对裁后可以得到两张A3纸，…，An纸对裁后可以得到两张An+1纸．

（1）填空：A1纸面积是A2纸面积的几倍，A2纸周长是A4纸周长的几倍；

（2）根据An系列纸张的规格特征，求出该系列纸张的长与宽（长大于宽）之比；

（3）设A1纸张的重量为a克，试求出A8纸张的重量．（用含a的代数式表示）

【题目】如图，在Rt△ABC中，∠ACB＝90°，D是AC上一点，过B，C，D三点的⊙O交AB于点E，连接ED，EC，点F是线段AE上的一点，连接FD，其中∠FDE＝∠DCE．

（1）求证：DF是⊙O的切线．

（2）若D是AC的中点，∠A＝30°，BC＝4，求DF的长．

【题目】如图，在平面直角坐标系中，边长为的正方形ABCD的顶点A，B在x轴上，连接OD、BD、△BOD的外心I在中线BF上，BF与AD交于点E，连接OE，若点M是直线BF上的一动点，且△BMD与△OED相似，则点M的坐标_____．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网