题目内容
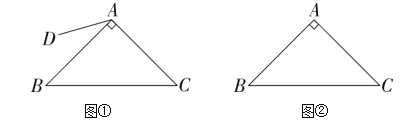
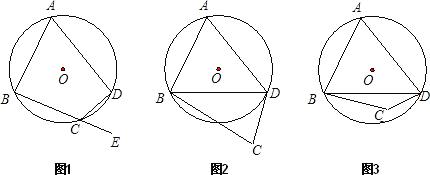
【题目】(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
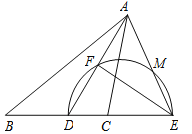
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
【答案】(1)见解析;(2)①∠A+∠BCD<180°,②∠A+∠BCD>180°.
【解析】
(1)连接AC,BD,由同弧所对的圆周角相等与四边形的内角和为360°,即可证得∠A+∠BCD=180°;又由同角的补角相等,求得∠DCE=∠A;
(2)根据圆的内接四边形的对角互补与三角形的外角的性质,即可证得结论.
(1)证明:连结AC,BD,

∴∠CAD=∠CBD,∠ABD=∠ACD,∠ADB=∠ACB,∠BAC=∠BDC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠CAD+∠BAC+∠ABD+∠CBD+∠ACB+∠ACD+∠ADB+∠BDC=360°,
∴∠CAD+∠BAC+∠ACB+∠ACD=180°,
即∠BAD+∠BCD=180°,
又∵∠DCE+∠BCD=180°,
∴∠DCE=∠BAD.
(2)解:①设BC与⊙O交于点E,连结DE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BED=∠CDE+∠BCD,
∴∠BED>∠BCD,
∴∠A+∠BCD<180°.
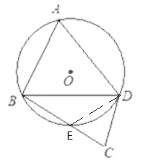
②延长DC交⊙O于点E,连结BE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BCD=∠CBE+∠BED,
∴∠BCD>∠BED,
∴∠A+∠BCD>180°.


练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目