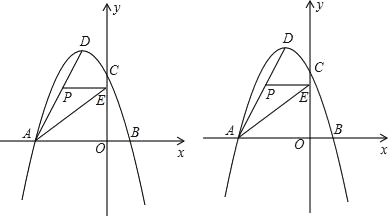题目内容
【题目】一段抛物线C：y＝﹣x2+3x+m（0≤x≤3）与直线y＝x+1有唯一公共点，若m为整数，则符合条件的所有m的值的和为_____．
【答案】9
【解析】
分两种情况进行讨论，①当抛物线与直线相切，△=0求得m=0，②当抛物线与直线不相切，但在0≤x≤3上只有一个交点时，找到两个临界值点，可得m=2，3，4，故m=0，2，3，4，然后求得它们的和即可．
解：∵抛物线C：y＝﹣x2+3x+m（0≤x≤3）与直线y＝x+1有唯一公共点
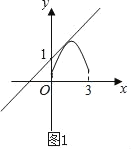
∴①如图1，抛物线与直线相切，
联立解析式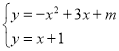
得x2﹣2x+1﹣m＝0
△＝（﹣2）2﹣4（1﹣m）＝0
解得m＝0
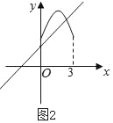
②如图2，抛物线与直线不相切，但在0≤x≤3上只有一个交点
此时两个临界值分别为（0，1）和（3，4）在抛物线上，
∴m的最小值＝1，但取不到，c的最大值＝4，能取到，
∴1＜m≤4，
又∵m为整数，
∴m＝2，3，4，
综上，m＝0，2，3，4，
0+2+3+4＝9，
故答案为9．
练习册系列答案
相关题目
