Question

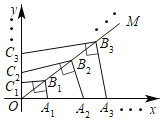
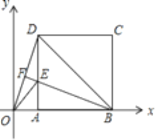
【题目】如图，在平面直角坐标系中，边长为的正方形ABCD的顶点A，B在x轴上，连接OD、BD、△BOD的外心I在中线BF上，BF与AD交于点E，连接OE，若点M是直线BF上的一动点，且△BMD与△OED相似，则点M的坐标_____．

Answer 1

【答案】（1，﹣1）或（﹣，）

【解析】

如图，连接AC交BF于M1，延长CD、BF交于点M2，直线BM2与y轴交于点N，连接DM1，OM1．首先证明点M1，M2是满足条件的点．然后求出它们的坐标即可．

解：如图，连接AC交BF于M1，延长CD、BF交于点M2，直线BM2与y轴交于点N，连接DM1，OM1．

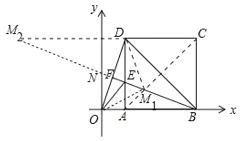
∵∠DBF＝∠FBO＝∠EDO＝∠EOD＝22.5°，

∴△BDM1∽△ODE，△BDM2∽△DEO，

∵B（2，0），M2（，），

∴直线BM2的解析式为y＝（＋1）x＋22．

∴点N（0，22），

∵M1D＝M1B＝M1O，

∴∠M1OB＝∠M1BO，

∵∠M1OB＋∠NOM1＝90°，∠ONB＋∠OBN＝90°，

∴∠ONB＝∠NOM1，

∴OM1＝NM1＝M1B，

∴M1（1，1），

∴满足条件的点M的坐标为（1，1）或（，）．

故答案为（1，1）或（，）．