题目内容
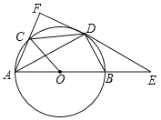
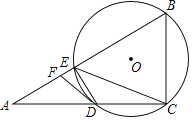
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
【答案】(1)见解析;(2)DF=![]() .
.
【解析】
(1)可证得BD是⊙O的直径,∠BCE=∠BDE,则∠BDE+∠FDE=90°,结论得证;
(2)先求出AC长,再求DE长,在Rt△BCD中求出BD长,在Rt△BED中求出BE长,证得△FDE∽△DBE,由比例线段![]() 可求出DF长.
可求出DF长.
解:(1)∵∠ACB=90°,点B,D在⊙O上,
∴BD是⊙O的直径,∠BCE=∠BDE,
∵∠FDE=∠DCE,∠BCE+∠DCE=∠ACB=90°,
∴∠BDE+∠FDE=90°,
即∠BDF=90°,
∴DF⊥BD,
又∵BD是⊙O的直径,
∴DF是⊙O的切线.
(2)如图,∵∠ACB=90°,∠A=30°,BC=4,
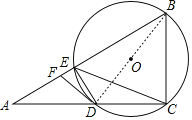
∴AB=2BC=2×4=8,
∴![]() ,
,
∵点D是AC的中点,
∴![]() ,
,
∵BD是⊙O的直径,
∴∠DEB=90°,
∴∠DEA=180°﹣∠DEB=90°,
∴![]() ,
,
在Rt△BCD中, ![]() ,
,
在Rt△BED中,![]() ,
,
∵∠FDE=∠DCE,∠DCE=∠DBE,
∴∠FDE=∠DBE,
∵∠DEF=∠BED=90°,
∴△FDE∽△DBE,
∴![]() ,即
,即![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
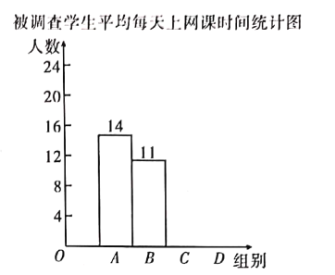
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.