题目内容
已知有两张全等的矩形纸片。
(1)将两张纸片叠合成如图甲,请判断四边形 的形状,并说明理由;
的形状,并说明理由;

(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形 的面积.
的面积.

(1)将两张纸片叠合成如图甲,请判断四边形
 的形状,并说明理由;
的形状,并说明理由;
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形
 的面积.
的面积.
解(1)四边形 是菱形。
是菱形。
理由:作AP⊥BC于P,AQ⊥CD于Q
由题意知:AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
∵两个矩形全等
∴AP=AQ
∵AP·BC=AQ·CD ∴BC=CD
∴平行四边形ABCD是菱形

(2)设BC=x,则CG=6-x ,CD=BC=x
在Rt△CDG中,
∴ 解得 x=
解得 x=
∴ S=BC·DG=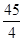
 是菱形。
是菱形。理由:作AP⊥BC于P,AQ⊥CD于Q
由题意知:AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
∵两个矩形全等
∴AP=AQ
∵AP·BC=AQ·CD ∴BC=CD
∴平行四边形ABCD是菱形

(2)设BC=x,则CG=6-x ,CD=BC=x
在Rt△CDG中,

∴
 解得 x=
解得 x=
∴ S=BC·DG=
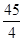
(1)作AP⊥BC于P,AQ⊥CD于Q,根据题意先证出四边形ABCD是平行四边形,再由AP=AQ得平行四边形ABCD是菱形;
(2)设BC=x,则CG=6-x,CD=BC=x,在Rt△CDG中,由勾股定理得出x,再求得面积.
(2)设BC=x,则CG=6-x,CD=BC=x,在Rt△CDG中,由勾股定理得出x,再求得面积.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
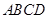 中,
中,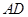 ∥
∥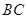 ,
,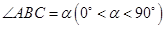 ,
,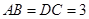 ,
,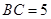 .点
.点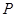 为射线
为射线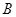 、
、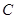 重合),点
重合),点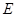 在直线
在直线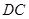 上,且
上,且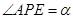 .记
.记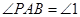 ,
,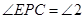 ,
,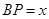 ,
,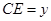 .
.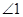 与
与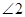 的数量关系;
的数量关系;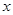 的取值范围;
的取值范围;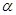 =
=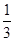 ,试用
,试用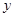 .
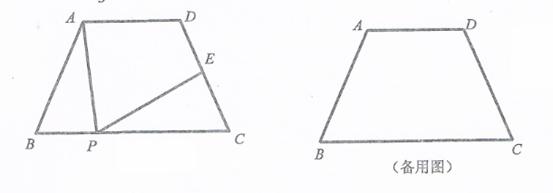
.
 中,
中,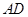 ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
 ;
; 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由. 的周长比
的周长比 的周长大7cm,则CD的长是 cm.
的周长大7cm,则CD的长是 cm. 90°,BD⊥DC,BD=DC,CE平分
90°,BD⊥DC,BD=DC,CE平分 ,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②
,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②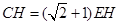 ;③
;③ ,其中正确的是( )
,其中正确的是( )