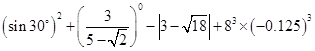题目内容
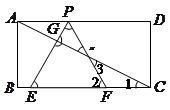
如图,已知矩形ABCD,AB= ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.

(1)求△PEF的边长;
(2)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有什么数量关系?并证明你猜想的结论.
 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
(1)求△PEF的边长;
(2)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有什么数量关系?并证明你猜想的结论.
(1)2(2)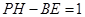 ,证明见解析
,证明见解析
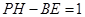 ,证明见解析
,证明见解析解: (1)过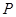 作
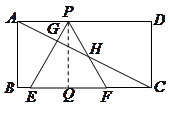
作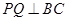 于
于
 矩形
矩形
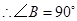 ,即
,即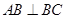 ,又
,又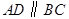
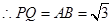 ………………1分
………………1分
 是等边三角形
是等边三角形
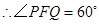
在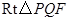 中
中
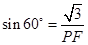
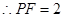
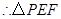 的边长为
的边长为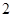 . ……………………………3分
. ……………………………3分
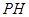 与
与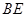 的数量关系是:
的数量关系是: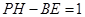 ………4分
………4分
在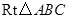 中,
中,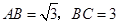
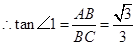
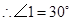 …………………………………5分
…………………………………5分
 是等边三角形
是等边三角形
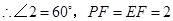 ……………………………6分
……………………………6分

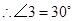
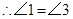
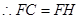 …………………………………………8分
…………………………………………8分
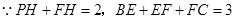
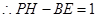 ……………………………………………9分
……………………………………………9分
(1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)猜想:PH-BE=1.利用∠ACB的正切值可求出∠ACB的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.
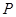 作
作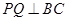 于
于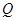

 矩形
矩形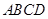
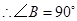 ,即
,即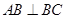 ,又
,又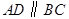
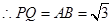 ………………1分
………………1分 是等边三角形
是等边三角形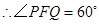
在
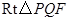 中
中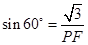
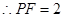
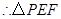 的边长为
的边长为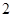 . ……………………………3分
. ……………………………3分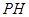 与
与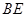 的数量关系是:
的数量关系是: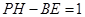 ………4分
………4分在
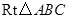 中,
中,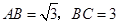

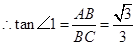
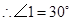 …………………………………5分
…………………………………5分 是等边三角形
是等边三角形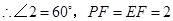 ……………………………6分
……………………………6分
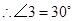
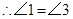
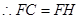 …………………………………………8分
…………………………………………8分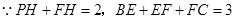
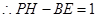 ……………………………………………9分
……………………………………………9分(1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)猜想:PH-BE=1.利用∠ACB的正切值可求出∠ACB的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.

练习册系列答案
相关题目
 .如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=
.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC= ,AC与y轴交于点E.
,AC与y轴交于点E.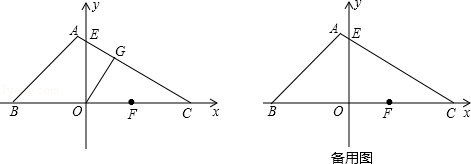
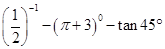
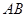 ,请用直尺和圆规作出线段
,请用直尺和圆规作出线段
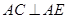 ,
,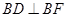 ,
,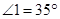 ,
, .求证:
.求证: .
.
 ≈1.732,结果保留整数).
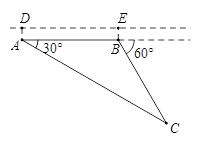
≈1.732,结果保留整数).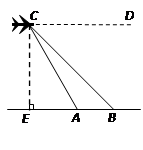
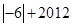 0+(-
0+(- )
)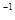 -8cos60°
-8cos60°