题目内容
如图,在梯形ABCD中,AD // BC,∠ABC = 90°,AB = 4,AD = 3,BC = 5,点M是边CD的中点,联结AM、BM.
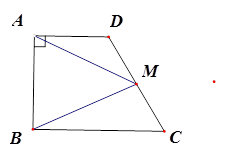
求:(1)△ABM的面积;
(2)∠MBC的正弦值.

求:(1)△ABM的面积;
(2)∠MBC的正弦值.
(1)8(2)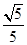
(1)延长AM交BC的延长线于点N,
∵AD∥BC,
∴∠DAM=∠N,∠D=∠MCN,
∵点M是边CD的中点,
∴DM=CM,
∴△ADM≌△NCM(AAS),
∴CN=AD=3,AM=MN=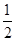 AN,
AN,
∴BN=BC+CN=5+3=8,
∵∠ABC=90°,
∴S△ABN=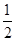 ×AB•BN=
×AB•BN=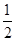 ×4×8=16,
×4×8=16,
∴S△ABM=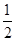 S△ABN=8;
S△ABN=8;
∴△ABM的面积为8;………………………………4分
(2)过点M作MK⊥BC,
∵∠ABC=90°,
∴MK∥AB,
∴△NMK∽△NAB,
∴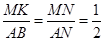 ,
,
∴MK=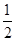 AB=2,
AB=2,
在Rt△ABN中,AN=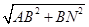 =
=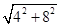 =4
=4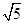 ,
,
∴BM=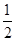 AN=2
AN=2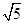 ,
,
在Rt△BKM中,sin∠MBC=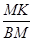 =
=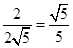 .
.
∴∠MBC的正弦值为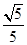 .………………………………4分
.………………………………4分
(1)首先作辅助线:延长AM交BC的延长线于点N,然后利用梯形的性质,即可证得△ADM≌△NCM(AAS),根据全等三角形的性质,即可求得CN的长,即可求得Rt△ABN的面积,则可求得△ABM的面积;
(2)作辅助线:过点M作MK⊥BC,构造Rt△BKM,即可求得∠MBC的正弦值.

∵AD∥BC,
∴∠DAM=∠N,∠D=∠MCN,
∵点M是边CD的中点,
∴DM=CM,
∴△ADM≌△NCM(AAS),
∴CN=AD=3,AM=MN=
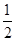 AN,
AN,∴BN=BC+CN=5+3=8,
∵∠ABC=90°,
∴S△ABN=
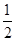 ×AB•BN=
×AB•BN=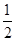 ×4×8=16,
×4×8=16,∴S△ABM=
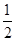 S△ABN=8;
S△ABN=8;∴△ABM的面积为8;………………………………4分
(2)过点M作MK⊥BC,

∵∠ABC=90°,
∴MK∥AB,
∴△NMK∽△NAB,
∴
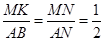 ,
,∴MK=
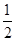 AB=2,
AB=2,在Rt△ABN中,AN=
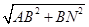 =
=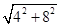 =4
=4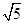 ,
,∴BM=
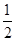 AN=2
AN=2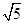 ,
,在Rt△BKM中,sin∠MBC=
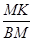 =
=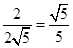 .
.∴∠MBC的正弦值为
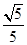 .………………………………4分
.………………………………4分(1)首先作辅助线:延长AM交BC的延长线于点N,然后利用梯形的性质,即可证得△ADM≌△NCM(AAS),根据全等三角形的性质,即可求得CN的长,即可求得Rt△ABN的面积,则可求得△ABM的面积;
(2)作辅助线:过点M作MK⊥BC,构造Rt△BKM,即可求得∠MBC的正弦值.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
 。
。
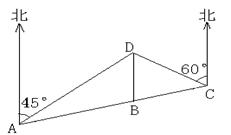
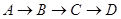 的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西
的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西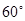 方向。C市在A市北偏东
方向。C市在A市北偏东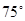 方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据:
方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据: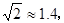
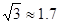 )
)
 是放置在正方形网格中的一个角,点A,B,C都在格点上,则
是放置在正方形网格中的一个角,点A,B,C都在格点上,则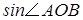 的值是 ▲ .
的值是 ▲ .
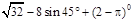
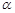 ,若cot
,若cot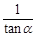 ,则cot45°= .
,则cot45°= . 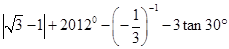 .
.