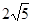题目内容
在△ABC中,∠ABC=45°,tan∠ACB=
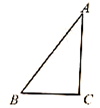
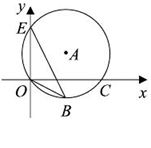
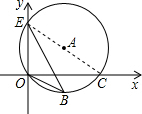
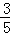 .如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=
.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC= ,AC与y轴交于点E.
,AC与y轴交于点E.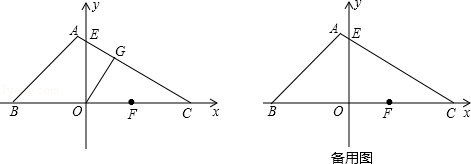
(1)求AC所在直线的函数解析式;
(2)过点O作OG⊥AC,垂足为G,求△OEG的面积;
(3)已知点F(10,0),在△ABC的边上取两点P,Q,是否存在以O,P,Q为顶点的三角形与△OFP全等,且这两个三角形在OP的异侧?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
解:(1) 在Rt△OCE中,OE=OCtan∠OCE=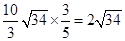 ,∴点E(0,
,∴点E(0,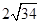 。
。
设直线AC的函数解析式为y=kx+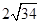 ,有
,有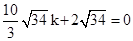 ,解得:k=
,解得:k=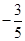 。
。
∴直线AC的函数解析式为y=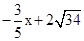 。
。
(2) 在Rt△OGE中,tan∠EOG=tan∠OCE=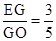 ,
,
设EG=3t,OG=5t,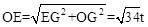 ,∴
,∴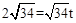 ,得t=2。
,得t=2。
∴EG=6,OG=10。∴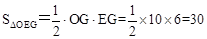 /
/
(3) 存在。
①当点Q在AC上时,点Q即为点G,
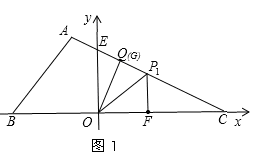
如图1,作∠FOQ的角平分线交CE于点P1,
由△OP1F≌△OP1Q,则有P1F⊥x轴,
由于点P1在直线AC上,当x=10时,
y=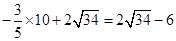
∴点P1(10,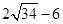 )。
)。
②当点Q在AB上时,如图2,
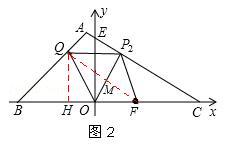
有OQ=OF,作∠FOQ的角平分线交CE于点P2,过点Q作QH⊥OB于点H,设OH=a,
则BH=QH=14-a,
在Rt△OQH中,a2+(14-a)2=100,
解得:a1=6,a2=8,∴Q(-6,8)或Q(-8,6)。
连接QF交OP2于点M.
当Q(-6,8)时,则点M(2,4);当Q(-8,6)时,则点M(1,3)。
设直线OP2的解析式为y=kx,则2k=4,k=2。∴y=2x。
解方程组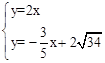 ,得
,得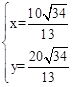 。
。
∴P2(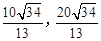 );
);
当Q(-8,6)时,则点M(1,3).同理可求P2′(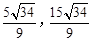 )。
)。
综上所述,满足条件的P点坐标为
(10,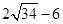 )或(
)或(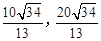 )或(
)或(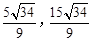 )。
)。
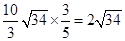 ,∴点E(0,
,∴点E(0,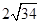 。
。设直线AC的函数解析式为y=kx+
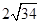 ,有
,有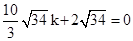 ,解得:k=
,解得:k=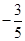 。
。∴直线AC的函数解析式为y=
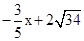 。
。(2) 在Rt△OGE中,tan∠EOG=tan∠OCE=
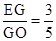 ,
,设EG=3t,OG=5t,
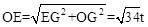 ,∴
,∴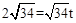 ,得t=2。
,得t=2。∴EG=6,OG=10。∴
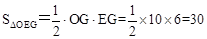 /
/(3) 存在。
①当点Q在AC上时,点Q即为点G,

如图1,作∠FOQ的角平分线交CE于点P1,
由△OP1F≌△OP1Q,则有P1F⊥x轴,
由于点P1在直线AC上,当x=10时,
y=
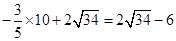
∴点P1(10,
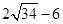 )。
)。②当点Q在AB上时,如图2,

有OQ=OF,作∠FOQ的角平分线交CE于点P2,过点Q作QH⊥OB于点H,设OH=a,
则BH=QH=14-a,
在Rt△OQH中,a2+(14-a)2=100,
解得:a1=6,a2=8,∴Q(-6,8)或Q(-8,6)。
连接QF交OP2于点M.
当Q(-6,8)时,则点M(2,4);当Q(-8,6)时,则点M(1,3)。
设直线OP2的解析式为y=kx,则2k=4,k=2。∴y=2x。
解方程组
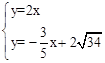 ,得
,得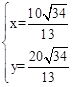 。
。∴P2(
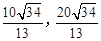 );
);当Q(-8,6)时,则点M(1,3).同理可求P2′(
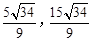 )。
)。综上所述,满足条件的P点坐标为
(10,
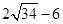 )或(
)或(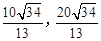 )或(
)或(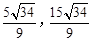 )。
)。(1)根据三角函数求E点坐标,运用待定系数法求解。
(2)在Rt△OGE中,运用三角函数和勾股定理求EG,OG的长度,再计算面积。
(3)分两种情况讨论求解:①点Q在AC上;②点Q在AB上.求直线OP与直线AC的交点坐标即可。
(2)在Rt△OGE中,运用三角函数和勾股定理求EG,OG的长度,再计算面积。
(3)分两种情况讨论求解:①点Q在AC上;②点Q在AB上.求直线OP与直线AC的交点坐标即可。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

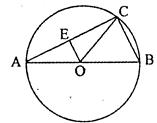
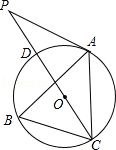
 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
 。
。
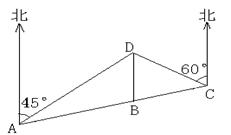
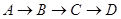 的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西
的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西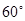 方向。C市在A市北偏东
方向。C市在A市北偏东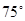 方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据:
方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据: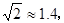
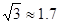 )
)
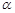 ,若cot
,若cot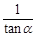 ,则cot45°= .
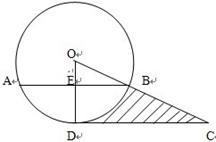
,则cot45°= . 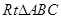 中,
中,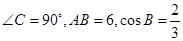 ,则
,则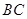 的长为
的长为