题目内容
【题目】如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(5,3),抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M、B、D为顶点的三角形的面积是6,求点M的坐标;
(3)点P从点D出发,以每秒1个单位长度的速度沿D→B匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度沿B→A→D匀速运动,当点P到达点B时,P、Q同时停止运动,设运动的时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是等腰三角形?请直接写出所有符合条件的值.
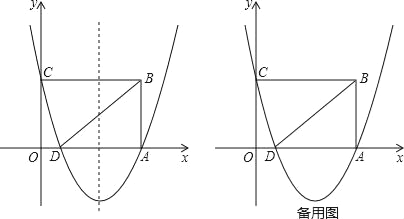
【答案】(1)y=![]() x2
x2![]() x+3;(2)点M的坐标为(3,
x+3;(2)点M的坐标为(3,![]() )或(3,
)或(3,![]() );(3)当t=
);(3)当t=![]() ,t=
,t=![]() 或t=
或t=![]() 时,以D、P、Q为顶点的三角形是等腰三角形.
时,以D、P、Q为顶点的三角形是等腰三角形.
【解析】
(1)求出点A、C的坐标,利用待定系数法求出抛物线的解析式;
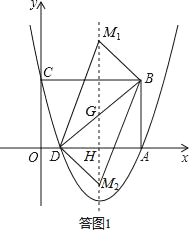
(2)如答图1所示,关键是求出MG的长度,利用面积公式解决;注意,符合条件的点M有2个,不要漏解;
(3)△DPQ为等腰三角形,可能有三种情形,需要分类讨论:
①若PD=PQ,如答图2所示;
②若PD=DQ,如答图3所示;
③若PQ=DQ,如答图4所示.
(1)∵矩形ABCD,B(5,3),
∴A(5,0),C(0,3).
∵点A(5,0),C(0,3)在抛物线y=![]() x2+bx+c上,
x2+bx+c上,
∴ ,解得:b=
,解得:b=![]() ,c=3.
,c=3.
∴抛物线的解析式为:y=![]() x2
x2![]() x+3.
x+3.
(2)如答图1所示,
∵y=![]() x2
x2![]() x+3=
x+3=![]() (x﹣3)2
(x﹣3)2![]() ,
,
∴抛物线的对称轴为直线x=3.
如答图1所示,设对称轴与BD交于点G,与x轴交于点H,则H(3,0).
令y=0,即![]() x2
x2![]() x+3=0,解得x=1或x=5.
x+3=0,解得x=1或x=5.
∴D(1,0),∴DH=2,AH=2,AD=4.
∵tan∠ADB=![]() ,∴GH=DHtan∠ADB=2×
,∴GH=DHtan∠ADB=2×![]() ,
,
∴G(3,![]() ).
).
∵S△MBD=6,即S△MDG+S△MBG=6,
∴![]() MGDH+
MGDH+![]() MGAH=6,
MGAH=6,
即:![]() MG×2+
MG×2+![]() MG×2=6,
MG×2=6,
解得:MG=3.
∴点M的坐标为(3,![]() )或(3,-
)或(3,-![]() ).
).
(3)在Rt△ABD中,AB=3,AD=4,则BD=5,∴sinB=![]() ,cosB=
,cosB=![]() .
.
以D、P、Q为顶点的三角形是等腰三角形,则:
①若PD=PQ,如答图2所示:
此时有PD=PQ=BQ=t,过点Q作QE⊥BD于点E,
则BE=PE,BE=BQcosB=![]() t,QE=BQsinB=
t,QE=BQsinB=![]() t,
t,
∴DE=t+![]() t=
t=![]() t.
t.
由勾股定理得:DQ2=DE2+QE2=AD2+AQ2,
即(![]() t)2+(
t)2+(![]() t)2=42+(3﹣t)2,
t)2=42+(3﹣t)2,
整理得:![]() t2+6t﹣25=0,
t2+6t﹣25=0,
解得:t=![]() 或t=﹣5(舍去),
或t=﹣5(舍去),
∴t=![]() ;
;
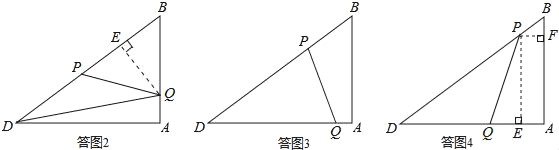
②若PD=DQ,如答图3所示:
此时PD=t,DQ=AB+AD﹣t=7﹣t,
∴t=7﹣t,
∴t=![]() ;
;
③若PQ=DQ,如答图4所示:
∵PD=t,∴BP=5﹣t;
∵DQ=7﹣t,∴PQ=7﹣t,AQ=4﹣(7﹣t)=t﹣3.
过点P作PF⊥AB于点F,则PF=PBsinB=(5﹣t)×![]() =4﹣
=4﹣![]() t,BF=PBcosB=(5﹣t)×
t,BF=PBcosB=(5﹣t)×![]() =3﹣
=3﹣![]() t.
t.
∴AF=AB﹣BF=3﹣(3﹣![]() t)=
t)=![]() t.
t.
过点P作PE⊥AD于点E,则PEAF为矩形,
∴PE=AF=![]() t,AE=PF=4﹣
t,AE=PF=4﹣![]() t,∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣
t,∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣![]() t)=
t)=![]() t﹣7.
t﹣7.
在Rt△PQE中,由勾股定理得:EQ2+PE2=PQ2,
即:(![]() t﹣7)2+(
t﹣7)2+(![]() t)2=(7﹣t)2,
t)2=(7﹣t)2,
整理得:13t2﹣56t=0,
解得:t=0(舍去)或t=![]() .
.
∴t=![]() .
.
综上所述,当t=![]() ,t=
,t=![]() 或t=
或t=![]() 时,以D、P、Q为顶点的三角形是等腰三角形.
时,以D、P、Q为顶点的三角形是等腰三角形.

 口算能手系列答案
口算能手系列答案