题目内容
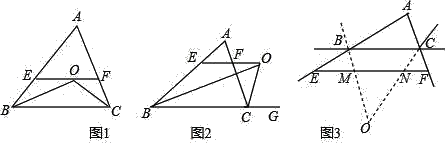
【题目】已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F
(1)直接写出图1中所有的等腰三角形.指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=15,AC=10,求△AEF的周长;
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
(4)如图3,∠ABC、∠ACB的外角平分线的延长线相交于点O,请直接写出EF,BE,CF,MN之间的数量关系.不需证明.
【答案】(1)△BEO、△CFO是等腰三角形,EF= BE+CF;(2)25;(3)(1)中结论不成立,新结论为:EF=BE﹣CF,理由见解析;(4)EF=BE+MN+CF.
【解析】
(1)利用角平分线和平行线的即可得出结论;
(2)利用(1)的结论即可得出结论;
(3)同(1)的方法即可得出结论;
(4)同(1)的方法即可得出结论.
(1)∵BO是∠ABC的平分线,∴∠EBO=∠CBO.
∵EF∥BC,∴∠CBO=∠BOE,∴∠EBO=∠EOB,∴BE=OE,∴△BEO是等腰三角形.
同理:△CFO是等腰三角形,EF=OE+OF=BE+CF;
(2)由(1)知,OE=BE,OF=CF,∴AEF的周长为AE+EF+AF=AE+OE+OF+AF=AE+BE+CF+AF=AB+AC=25;
(3)(1)中结论不成立,新结论为:EF=BE﹣CF,理由:
∵BO是∠ABC的平分线,∴∠ABO=∠CBO.
∵EF∥BC,∴∠CBO=∠EOB,∴∠ABO=EOB,∴OE=BE.
同理:CF=OF,∴EF=OE﹣OF=BE﹣CF.
(4)∵BO是∠CBE的平分线,∴∠EBO=∠CBO.
∵EF∥BC,∴∠EMB=∠CBO,∴∠EBM=∠EMB,∴BE=EM,同理:FN=CF,∴EF=EM+MN+FN=BE+MN+CF.