题目内容
【题目】在平面直角坐标系中,已知A(1,1)、B(3,5),要在x轴上找一点P,使得△PAB的周长最小,则点P的坐标为 .
【答案】(0,2).
【解析】
试题解析:∵线段AB的长度是确定的,
∴△PAB的周长最小就是PA+PB的值最小,
∵3<5,
∴点P在y轴上,
如图1,作点A关于y轴的对称点A′,连接A′B交y轴于点P,
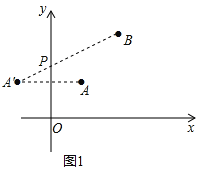
∵A(1,1),
∴A′(-1,1),
设直线A′B的解析式为y=kx+b(k≠0),
∴![]() ,解得
,解得![]() ,
,
∴直线A′B的解析式为y=x+2,
当x=0时,y=2,
∴P(0,2).
A′B=![]() ;
;
如图2,作点A关于x轴的对称点A′,连接A′B交y轴于点P,
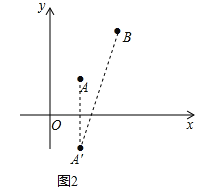
∵A(1,1),
∴A′(1,-1),
设直线A′B的解析式为y=kx+b(k≠0),
∴![]() ,解得
,解得![]() ,
,
∴直线A′B的解析式为y=3x-4,
当y=0时,x=![]() ,
,
∴P(![]() ,0).
,0).
A′B=![]() .
.
∵![]() <
<![]() .
.
故点P的坐标为(0,2).

练习册系列答案
相关题目


