题目内容
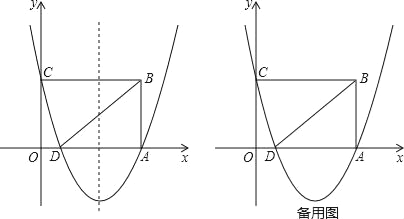
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求点P的坐标.

【答案】(3,4)或(2,4)或(8,4)
【解析】
因为题中没有指明△ODP的腰长与底分别是哪个边,故应该分情况进行分析,从而求得点P的坐标.
(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=![]() =3,则P的坐标是(3,4);
=3,则P的坐标是(3,4);
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
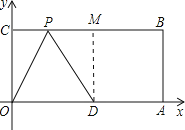
在直角△PDM中,PM=![]() =3,
=3,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).

【题目】某班级45名同学自发筹集到1700元资金,用于初中毕业时各项活动的经费,计划将资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品,已知每件文化衫28元,每本相册20元.
设购买的文化衫件数为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
购买的文化衫件数(件) | 5 | 10 | 20 | 30 | … |
买文化衫所学费用(元) | 140 |
| 560 |
| … |
买相册所需费用(元) | 800 |
| 500 |
| … |
(Ⅱ)设购买文化衫和相册所需费用共W元,求W与购买的文化衫件数x的函数关系式;
(Ⅲ)通过商议,决定拿出不少于540元旦不超过570元的资金用于请专业人士牌照,其余则用于购买文化衫和相册,购买文化衫和相册有哪几种方案?为使拍照的资金更充足,应选择哪种方案,并说明理由.