题目内容
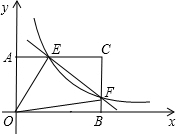
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=
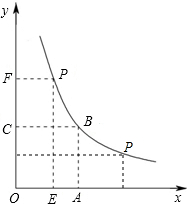
(k>0,x>0)的图象上,点P(m、n)是函数y=
(k>0,x>0)图象上的一个动点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设两个四边形OEPF和OABC不重合部分的面积之和为S.
(1)求B点坐标和k的值;
(2)当S=
时,求点P的坐标.

| k |
| x |
| k |
| x |
(1)求B点坐标和k的值;
(2)当S=
| 9 |
| 2 |

(1)∵正方形OABC的面积为9,
∴OA=OC=3,
∴B点的坐标为:(3,3),
∵点B在函数y=
(k>0,x>0)的图象上,
∴k=xy=9;
(2)∵P(m、n)是函数y=
图象上的一个动点,
∴mn=k=9,
当S=
时,P点的位置有两种情况:
第一种:P点在B点的左侧,这时,
即m=
,n=6,
P点坐标为:(
,6);
第二种:P点在B点的右侧,这时s=3(n-3)+3(3-m)=18-6m=
,
即n=
,m=6,P点坐标为:(6,
),
综上所述,P点的坐标为(
,6)或(6,
).
∴OA=OC=3,
∴B点的坐标为:(3,3),
∵点B在函数y=
| k |
| x |
∴k=xy=9;
(2)∵P(m、n)是函数y=
| k |
| x |
∴mn=k=9,
当S=
| 9 |
| 2 |
第一种:P点在B点的左侧,这时,
即m=
| 3 |
| 2 |
P点坐标为:(
| 3 |
| 2 |
第二种:P点在B点的右侧,这时s=3(n-3)+3(3-m)=18-6m=
| 9 |
| 2 |
即n=
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,P点的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |


练习册系列答案
相关题目
 标为4.
标为4.
 为(
为(