��Ŀ����
��ͼ������ABCD����A�ڵ�һ���ޣ���x����������ཻ��M����y�ĸ������ཻ��N��AB��x�ᣬ������������ͼ��y=
��A��C���㣬ֱ��AC��x���ཻ�ڵ�E����y���ཻ�ڵ�F��
��1����B��-3��3����ֱ��AC�Ľ���ʽΪy=ax+b��
����a��ֵ��
������OA��OC������OAC�������ΪS��OAC����ABC�������ΪS��ABC����S=S��ABC-S��OAC����S�Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
��2��AE��CF�Ƿ���ȣ���֤����Ľ��ۣ�

| k |
| x |
��1����B��-3��3����ֱ��AC�Ľ���ʽΪy=ax+b��
����a��ֵ��
������OA��OC������OAC�������ΪS��OAC����ABC�������ΪS��ABC����S=S��ABC-S��OAC����S�Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
��2��AE��CF�Ƿ���ȣ���֤����Ľ��ۣ�

��1���١��ı���ABCD�Ǿ��Σ���AB��x�ᣬB��-3��3����
��A��
��3����C��-3��-
����
��y=ax+b����A��C���㣬
��
����ȥb�ã���
+3��a=
+3��
��k��0����
+3��0����a=1��
��S=S��ABC-S��OAC=S��ACD-S��OAC=S��AOM+S��CON+S����ONDM��
��S=
+
+
=
��k+
��2-
��
�൱k��-
ʱ��S��k�����������
����k��0����kû����Сֵ��SҲû����Сֵ��
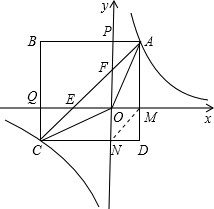
��2��AE=CF���������£�
����MN����AB��y��Ľ���ΪP��BC��x��Ľ���ΪQ��
��S����APOM=S����CQON=k��
��DN•AD=DM•CD����
=
��
�֡ߡ�D=��D��
���DNM����DCA���á�DNM=��DCA��
��MN��AC��
�֡�AD��y�ᣬ���ı���AFNM��ƽ���ı��Σ�
ͬ���ı���CNME��ƽ���ı��Σ�
��CE=MN=AF����AE=CF��
��A��
| k |
| 3 |
| k |
| 3 |
��y=ax+b����A��C���㣬
��
|
| k |
| 3 |
| k |
| 3 |
��k��0����
| k |
| 3 |
��S=S��ABC-S��OAC=S��ACD-S��OAC=S��AOM+S��CON+S����ONDM��
��S=
| k |
| 2 |
| k |
| 2 |
| k2 |
| 9 |
| 1 |
| 9 |
| 9 |
| 2 |
| 9 |
| 4 |
�൱k��-
| 9 |
| 2 |
����k��0����kû����Сֵ��SҲû����Сֵ��

��2��AE=CF���������£�
����MN����AB��y��Ľ���ΪP��BC��x��Ľ���ΪQ��
��S����APOM=S����CQON=k��
��DN•AD=DM•CD����
| DN |
| CD |
| DM |
| AD |
�֡ߡ�D=��D��
���DNM����DCA���á�DNM=��DCA��
��MN��AC��
�֡�AD��y�ᣬ���ı���AFNM��ƽ���ı��Σ�
ͬ���ı���CNME��ƽ���ı��Σ�
��CE=MN=AF����AE=CF��

��ϰ��ϵ�д�
 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
�����Ŀ

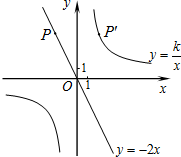 k��0����ͼ���ϣ�
k��0����ͼ���ϣ�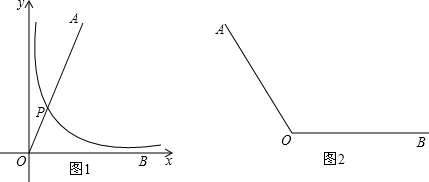

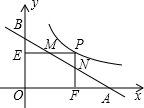
 ������______�ҵ������ʣ����������������=����
������______�ҵ������ʣ����������������=����