题目内容
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.
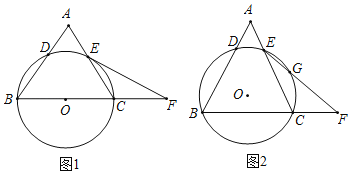
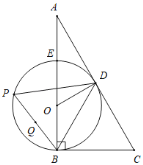
(1)如图1,BC为直径,求证:EF是⊙O的切线;
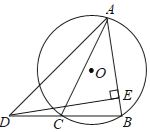
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)只要证明OE⊥EF即可;(2)如图2中,连接OB、OC、OE作CH⊥OB交BO的延长线于H.首先利用弧长公式求出∠BOC,解直角三角形求出BC、EC的长即可解决问题;
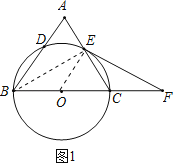
解:(1)证明:如图1中,连接BE、OE.
∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°,
∵BC是直径,
∴∠BEC=90°,
∴BE⊥AC,
∵BA=BC,
∴AE=EC=CF,
∴∠F=∠CEF,
∵∠BCE=∠F+∠CEF=60°,
∴∠CEF=∠F=30°,
∵OE=OC,∠OCE=60°,
∴△OEC是等边三角形,
∴∠OEC=60°,
∴∠OEF=60°+30°=90°.
∴OE⊥EF.
∴EF是⊙O的切线.
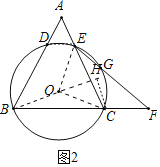
(2)解:如图2中,连接OB、OC、OE作CH⊥OB交BO的延长线于H.
∵![]() 的长=
的长=![]() ,
,
∴n=150°,
∴∠BOC=150°,∠OBC=∠OCB=15°,∠COH=30°,
在Rt△OCH中,CH=![]() OC=
OC=![]() ,OH=
,OH=![]() ,
,
∴BC=![]() ,
,
∵∠ECO=∠ACB﹣∠OCB=45°,
∴EC=![]() ,
,
∴AE=CF=![]() ,
,
∴BF=![]()
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目