题目内容

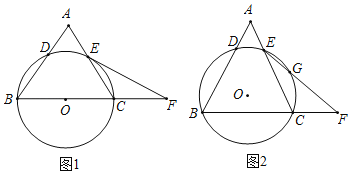
【题目】如图，在半径为6的⊙O中，正六边形ABCDEF与正方形AGDH都内接于⊙O，则图中阴影部分的面积为（　　）

A. 27﹣9B. 18C. 54﹣18D. 54

【答案】C

【解析】

设EF交AH于M、交HD于N，连接OF、OE、MN，根据题意得到△EFO是等边三角形，△HMN是等腰直角三角形，由三角函数求出△EFO的高，由三角形面积公式即可得出阴影部分的面积．

解：设EF交AH于M、交HD于N，连接OF、OE、MN，如图所示：

根据题意得：△EFO是等边三角形，△HMN是等腰直角三角形，

∴EF＝OF＝6，

∴△EFO的高为：OFsin60°＝6×＝，MN＝2（6﹣）＝12﹣，

∴FM＝（6﹣12+）＝﹣3，

∴阴影部分的面积＝4S△AFM＝4×（﹣3）×＝54﹣；

故选：C．

练习册系列答案
相关题目

【题目】甲、乙两车从A地出发，沿同一路线驶向B地．甲车先出发匀速驶向B地，40min后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时．由于满载货物，为了行驶安全，速度减少了50km/h，结果与甲车同时到达B地．甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示，则下列说法：①a=4.5；②甲的速度是60km/h；③乙出发80min追上甲；④乙刚到达货站时，甲距B地180km．其中正确是（　　）

A.B.C.D.

【题目】如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2.25m，喷出水流的运动路线是抛物线．水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3m．求水流的落地点C到水枪底部B的距离．

【题目】在一堂数学实践课上，赵老师给出了下列问题：

（提出问题）

（1）如图1，在△ABC中，E是BC的中点，P是AE的中点，就称CP是△ABC的“双中线”，∠ACB＝90°，AC＝3，AB＝5．则CP＝　 　．

（探究规律）

（2）在图2中，E是正方形ABCD一边上的中点，P是BE上的中点，则称AP是正方形ABCD的“双中线”，若AB＝4．则AP的长为　 　（按图示辅助线求解）；

（3）在图3中，AP是矩形ABCD的“双中线”，若AB＝4，BC＝6，请仿照（2）中的方法求出AP的长，并说明理由；

（拓展应用）

（4）在图4中，AP是平行四边形ABCD的“双中线”，若AB＝4，BC＝10，∠BAD＝120°．求出△ABP的周长，并说明理由？

【题目】关于x的一元二次方程x2+（2k+1）x+k2+1＝0．

（1）当方程有一个根为﹣1时，求k的值及另一个根；

（2）当方程有两个不相等的实数根，求k的取值范围；

（3）若方程两实根x1、x2满足x1+x2＝x1x2，求k的值．

【题目】在△ABC中，AC＝BC，∠ACB＝90°，直线l经过直角顶点C，AD⊥l，BE⊥l，垂足分别为D、E．

（1）如图，若AD＝1，BE＝3，求DE的长度．

（2）当直线l绕C点转动时，若AD＝a，BE＝b．请画出示意的图形并用含a、b的代数式直接表示出DE的长．

【题目】哈尔滨市滑雪业提前进入旺季，某体育用品商店购进一批简易滑雪板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.

（1）设商家每件售价x元，每星期的销售数量为y元，求y与x之间的函数关系式；

（2）降价后，商家要使每星期的销售利润W最大，应将售价定为多少元？最大销售利润是多少？

【题目】在等边△ABC中，以BC为弦的⊙O分别与AB，AC交于点D和E，点F是BC延长线上一点，CF＝AE，连接EF．

（1）如图1，BC为直径，求证：EF是⊙O的切线；

（2）如图2，EF与⊙O交于点G，⊙O的半径为1，BC的长为π，求BF的长．

【题目】我们县是紫菜生产大县，某景点商户向游客推销一种加工好的优质紫菜，已知每千克成本为20元.市场调查发现，在一段时间内，该产品销售量（千克）与销售单价（元/千克）的变化而变化有如下关系式：.设这种紫菜在这段时间内的销售利润为（元）.

（1）求与的关系式；

（2）当销售价定为多少元时，每天的销售利润最大？最大利润是多少？

（3）如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克，该商户每天能否获得比150元更大的利润？如果能请求出最大利润，如果不能，请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网