题目内容
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )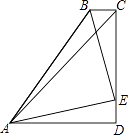
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
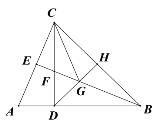
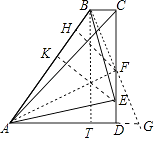
【解析】如图取CD的中点F,连接BF延长BF交AD的延长线于G,作FH⊥AB于H,EK⊥AB于K.作BT⊥AD于T.
∵BC∥AG,
∴∠BCF=∠FDG,
∵∠BFC=∠DFG,FC=DF,
∴△BCF≌△GDF,
∴BC=DG,BF=FG,
∵AB=BC+AD,AG=AD+DG=AD+BC,
∴AB=AG,∵BF=FG,
∴BF⊥AF,∠ABF=∠G=∠CBF,
∵FH⊥BA,FC⊥BC,
∴FH=FC,易证△FBC≌△FBH,△FAH≌△FAD,
∴BC=BH,AD=AH,
由题意AD=DC=4,设BC=TD=BH=x,
在Rt△ABT中,∵AB2=BT2+AT2,
∴(x+4)2=42+(4﹣x)2,
∴x=1,
∴BC=BH=TD=1,AB=5,
设AK=EK=y,DE=z,
∵AE2=AK2+EK2=AD2+DE2,BE2=BK2+KE2=BC2+EC2,
∴42+z2=2y2①,
(5﹣y)2+y2=12+(4﹣z)2②
由②得到25﹣10y+2y2=5﹣8z+z2③,
①代入③可得z= ![]() ④
④
④代入①可得y= ![]() (负根已经舍弃),
(负根已经舍弃),
∴S△ABE= ![]() ×5×
×5× ![]() =
= ![]() ,
,
所以答案是:D.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.

练习册系列答案
相关题目