��Ŀ����
����Ŀ����֪��A��B�ֱ���x�ᡢy���ϵĶ��㣬��C��D��ij������ͼ���ϵĵ㣬���ı���ABCD��A��B��C��D�����������У�Ϊ������ʱ�����dz����������Ϊ�˺���ͼ��ġ����������Ρ���
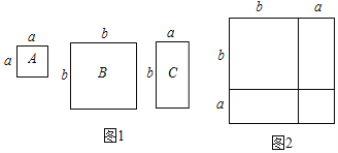
���磺��ͼ1�У�������ABCD��һ�κ���y=x+1ͼ�������һ�������������Ρ���
��1����ͼ1����ij������һ�κ���y=x+1��������ͼ������С����������Ρ��ı߳���
��2����ͼ2����ij�����Ƿ��������� ![]() ��k��0��������ͼ��ġ����������Ρ�ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ�������������Ľ���ʽ��
��k��0��������ͼ��ġ����������Ρ�ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ�������������Ľ���ʽ��
��3����ͼ3����ij�����Ƕ��κ���y=ax2+c��a��0��������ͼ��ġ����������Ρ�ΪABCD��C��D�е�һ��������Ϊ��3��4��������ֱ��д���ö��κ����Ľ���ʽ��
���𰸡�
��1���⣺��I������A��x�������ᡢ��B��y�Ḻ������ʱ��
������ABCD�ı߳�Ϊ ![]() ��
��
��II������A��x�Ḻ���ᡢ��B��y����������ʱ��
�������α߳�Ϊa����3a= ![]() ��
��
���a= ![]() ����ʱ�����εı߳�Ϊ
����ʱ�����εı߳�Ϊ ![]() ��
��
�������������Ρ��ı߳�Ϊ ![]() ��
�� ![]()
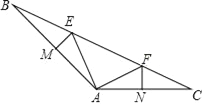
��2���⣺��ͼ����DE��x�ᣬCF��y�ᣬ����ֱ�Ϊ��E��F��
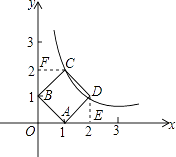
��֤��ADE�ա�BAO�ա�CBF��
�ߵ�D������Ϊ��2��m����m��2��
��DE=OA=BF=m��
��OB=AE=CF=2��m��
��OF=BF+OB=2��
���C��������2��m��2����
��2m=2��2��m�������m=1��
�෴���������Ľ���ʽΪy= ![]()
��3���⣺ʵ������������߿������ϵ���������У���һ���㶼�ڣ�3��4������࣬����������ʱ����һ�㶼�ڣ�3��4�����Ҳ࣬�������������Բ�����
a������A��x���������ϣ���B��y���������ϣ���C����Ϊ��3��4��ʱ������һ������Ϊ��4��1������Ӧ�ĺ�������ʽ��y=�� ![]() x2+
x2+ ![]() ��
��
b������A��x ���������ϣ��� B�� y���������ϣ���D ����Ϊ��3��4��ʱ�������ڣ�
c������A �� x ���������ϣ��� B�� y�Ḻ�����ϣ���C ����Ϊ��3��4��ʱ��������
d������A��x ���������ϣ���B��y�Ḻ�����ϣ���D����Ϊ��3��4��ʱ������һ������CΪ����1��3������Ӧ�ĺ����Ľ���ʽ��y= ![]() x2+
x2+ ![]() ��
��
e������A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���C����Ϊ��3��4��ʱ����һ������D�������ǣ�7����3��ʱ����Ӧ�ĺ�������ʽ��y=�� ![]() x2+
x2+ ![]() ��
��
f������A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���C����Ϊ��3��4��ʱ����һ������D�������ǣ���4��7��ʱ����Ӧ��������Ϊy= ![]() x2+
x2+ ![]() ��
��
�ʶ��κ����Ľ���ʽ�ֱ�Ϊ��y= ![]() x2+
x2+ ![]() ��y=��
��y=�� ![]() x2+
x2+ ![]() ��y=��
��y=�� ![]() x2+
x2+ ![]() ��y=
��y= ![]() x2+
x2+ ![]()
����������1������ȷ�ػ���ͼ�Σ������������ε�����ȷ����ص������Ӷ����������εı߳�.
��2����ΪABCDΪ�����Σ����Կ������ߵõ�����ֱ�������Σ����õ�D��2��m���������ʾ����C�����꣬�����m��ֵ �����ɵõ������������Ľ���ʽ��
��3���������߿��ڼȿ������ϣ�Ҳ�������£��������߿�������ʱ�������ε���һ������Ҳ�����������ϣ������ȿ����ڵ㣨3��4������ߣ�Ҳ�����ڵ㣨3��4�����ұߣ����㣨3��4����x�������ߣ�����ȫ��������ȷ���߶εij�����ȷ������������һ��������ꣻ�������߿�������ʱҲ��һ���ط�Ϊ������������ۣ����ɵõ�����Ľ��ۣ�
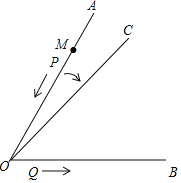
�����㾫����ͨ��������÷�����������ͼ��ͷ��������������ʣ����շ�����������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�㣻����:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ������������Խ����⣮

 ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�����Ŀ��ij��˾����Ƹһ�����ž������Լס��ҡ���������ѡ�˽������������ʲ��ԣ�������Գɼ��������ʾ��
������Ŀ | ���Գɼ� | ||
�� | �� | �� | |
רҵ֪ʶ | 74 | 87 | 90 |
�������� | 58 | 74 | 70 |
�ۺ����� | 87 | 43 | 50 |
��1������������β��Ե�ƽ���ɼ�ȷ����ѡ����ô˭����¼�ã�
��2������ʵ����Ҫ����˾��רҵ֪ʶ�������������ۺ�����������Ե÷ְ�4��3��1�ı���ȷ��ÿ���˵IJ����ܳɼ�����ʱ˭����¼�ã�
��3�����������רҵ֪ʶ�������������ۺ�����������Ե÷ֵı�����ȷ��ÿ���˵IJ����ܳɼ���ʹ���ұ�¼�ã���������Ƶı���Ϊx��y��1����x+y+1��10����x���� ����y���� ������д��x��y��һ������ֵ���ɣ���