Question

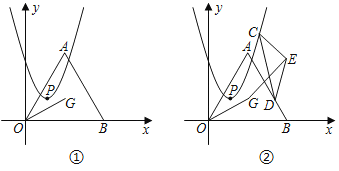
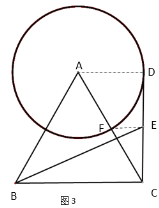
【题目】如图，等边△ABC中，AB=2，点D是以A为圆心，半径为1的圆上一动点，连接CD，取CD的中点E，连接BE，则线段BE的最大值与最小值之和为____．

Answer 1

【答案】

【解析】

取点D的特殊位置：当点D与点F重合时，当点D在CA延长线与圆A的交点时，当CD与圆A相切时，确定FE的长度都是0.5，从而得到点E的运动轨迹是以点F为圆心，0.5为半径的圆上运动，故而得到线段BE的最大值与最小值，由此得到答案．

∵△ABC为等边三角形，AB=2，

∴AC=AB=2，

设AC交圆A于点F，

∵点D是以A为圆心，半径为1的圆上一动点，

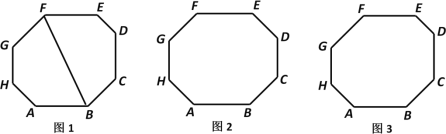
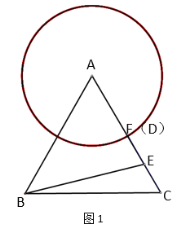
∴当点D与点F重合时，如图1，FE=0.5，

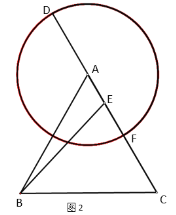
当点D在CA延长线与圆A的交点时,如图2，FE=0.5，

当CD与圆A相切时，FE=0.5，

故点E在以点F为圆心，0.5为半径的圆上运动，

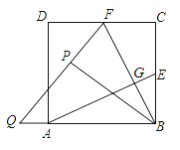
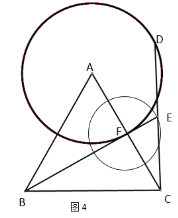
当点B、F、E三点共线时，线段BE有最大值和最小值，如图4：

∵AF=1，AC=2，

∴FC=1，

∴点F是AC的中点，

∵△ABC是等边三角形，

∴BF⊥AC，

∴BF= ，

线段BE的最大值=，最小值=，

∴线段BE的最大值与最小值之和为，

故答案为：．