题目内容
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
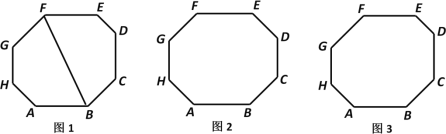
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
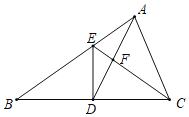
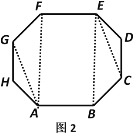
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
【答案】(1)①∠ABF+∠GFB=135°;②详见解析;③等角八边形的每一组正对边平行;(2)CD=GH,DE=HA,详见解析;(3)结论:至少需要已知5个内角为135°
【解析】
(1)①由等角八边形的概念可得它的每个内角均为135°,五边形BAHGF的内角和为540°,减去(∠A+∠H+∠G),即可求得结论;
②根据“内错角相等,两直线平行”即可证明;
③根据题目提供的信息,总结出结论即可;
(2)分别证明四边形ABEF是平行四边形,△AFG≌△EBC,△AGH≌△ECD即可得到结论;
(3)若4个内角等于135°,则每个内角不一定都为135°,若5个内角等于135°,其余各角的度数也是135°.
(1)①五边形BAHGF的内角和为(5-2)×180°=540°
∵∠A=∠H=∠G=![]()
∴∠ABF+∠GFB=540°-(∠A+∠H+∠G)=135°
即∠ABF+∠GFB=135°.
②∵∠1+∠4=135°,∠GFE=∠3+∠4=135°,
∴∠1=∠3,
∴AB∥EF.
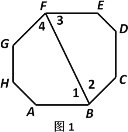
③等角八边形的每一组正对边平行.
(2)如图2,连结AF,BE,AG,CE,由①得:AB∥EF,
∵AB=EF,
∴四边形ABEF是平行四边形,
∴AF=BE,AF∥BE,
又∵BC∥FG,
∴∠AFG=∠EBC,
又∵BC=FG,
∴△AFG≌△EBC,
∴AG=EC,∠AGF=∠ECB,
∵∠HGF=∠BCD=135°,
∴∠AGH=∠ECD,
又∵∠H=∠D=135°,
∴△AGH≌△ECD,
∴CD=GH,DE=HA.
(3)结论:至少需要已知5个内角为135°.
①若4个内角等于135°,则每个内角不一定都为135°,
如图4,八边形ABCMNFPH不是等角八边形;
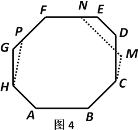
②若5个内角等于135°:
∵∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.
∴这八个角中,不论已知哪5个角是135°,都可以推导出其余的内角也是135°.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案