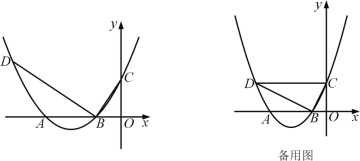Question

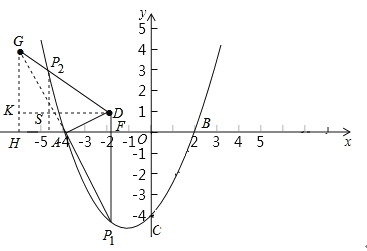
【题目】已知：在平面直角坐标系xOy中，二次函数y=mx 2 +2mx－4（m≠0）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，△ABC的面积为12．

（1）求这个二次函数的解析式；

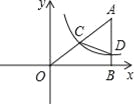
（2）点D的坐标为（－2，1），点P在二次函数的图象上，∠ADP为锐角，且tan∠ADP=2，求出点P的横坐标；

Answer 1

【答案】（1）y=x2+x-4；（2）点P横坐标为－2或

【解析】

（1）根据对称轴坐标公式可求二次函数图象的对称轴；当x＝0时，y＝﹣4，可求点C的坐标为（0，﹣4），根据三角形面积公式可求AB＝6．进一步得到A点和B点的坐标分别为（﹣4，0），（2，0）．待定系数法可求二次函数的解析式；

（2）作DF⊥x轴于点F．分两种情况：（ⅰ）当点P在直线AD的下方时；（ⅱ）当点P在直线AD的上方时，延长P1A至点G使得AG＝AP1，连接DG，作GH⊥x轴于点H，两种情况讨论可求点P1的坐标；

（1）由题意可得：该二次函数图象的对称轴为直线x＝﹣1；

∵当x＝0时，y＝﹣4，

∴点C的坐标为（0，﹣4），

∵S△ABC＝AB|yC|＝12，

∴AB＝6．

又∵点A，B关于直线x＝﹣1对称，

∴A点和B点的坐标分别为（﹣4，0），（2，0）．

∴4m+4m﹣4＝0，解得m＝．

∴所求二次函数的解析式为y＝x2+x﹣4．

（2）如图，作DF⊥x轴于点F．分两种情况：

（ⅰ）当点P在直线AD的下方时，如图所示．

由（1）得点A（﹣4，0），点D（﹣2，1），

∴DF＝1，AF＝2．

在Rt△ADF中，∠AFD＝90°，得tan∠ADF＝＝2．

延长DF与抛物线交于点P1，则P1点为所求．

∴点P1的坐标为（﹣2，﹣4）．

（ⅱ）当点P在直线AD的上方时，延长P1A至点G使得AG＝AP1，连接DG，作GH⊥x轴于点H，如图所示．

可证△GHA≌△P1FA．

∴HA＝AF，GH＝P1F，GA＝P1A．

又∵A（﹣4，0），P1（﹣2，﹣4），

∴点G的坐标是（﹣6，4）．

在△ADP1中，

DA＝，DP1＝5，

AP1＝2，

∴DA2+AP12＝DP12

∴∠DAP1＝90°．

∴DA⊥GP1．

∴DG＝DP1．

∴∠ADG＝∠ADP1．

∴tan∠ADG＝tan∠ADP1＝2．

设DG与抛物线的交点为P2，则P2点为所求．

作DK⊥GH于点K，作P2S∥GK交DK于点S．

设P2点的坐标为（x，x2+x﹣4），

则P2S＝x2+x﹣4﹣1＝x2+x﹣5，DS＝﹣2﹣x．

由＝，GK＝3，DK＝4，得＝．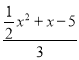

整理，得2x2+7x﹣14＝0．

解得x＝．

∵P2点在第二象限，

∴P2点的横坐标为x＝（舍正）．

综上，P点的横坐标为﹣2或．