题目内容
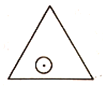
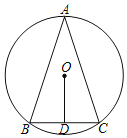
【题目】如图，△ABC内接于⊙O，AB＝AC＝2
，O到BC的距离为OD＝1，则⊙O的半径为_____．
【答案】
【解析】
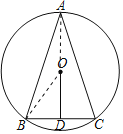
连接OA、OB，如图，先根据垂径定理和线段垂直平分线的性质得出点A、O、D三点共线，再设⊙O的半径为x，则AD＝x+1，BD2＝x2﹣1，然后在△ABD中根据勾股定理可得关于x的方程，解方程即得答案．
解：连接OA、OB，如图，
∵OD⊥BC，∴BD＝DC，
∴OD垂直平分BC，
∵AB＝AC，∴点A在直线OD上，
∴点A、O、D在同一条直线上，
设⊙O的半径为x，则AD＝x+1，
在△OBD中，OB2＝OD2+BD2，
∴BD2＝x2﹣1，
在△ABD中，AB2＝AD2+BD2，即（2
）2＝（x+1）2+x2﹣1，
解得，x1＝
（舍去），x2＝，
故答案为：．
练习册系列答案
相关题目
