题目内容
【题目】如图①，点G是等边三角形AOB的外心，点A在第一象限，点B坐标为(4，0)，连结OG．抛物线y＝ax（x﹣2）+1+
的顶点为P．
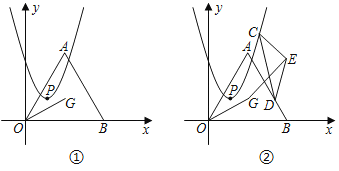
（1）直接写出点A的坐标与抛物线的对称轴；
（2）连结OP，求当∠AOG＝2∠AOP时a的值．
（3）如图②，若抛物线开口向上，点C，D分别为抛物线和线段AB上的动点，以CD为底边构造顶角为120°的等腰三角形CDE（点C，D，E成逆时针顺序），连结GE．
①点Q在x轴上，当四边形GDQO为平行四边形时，求GQ的值；
②当GE的最小值为1时，求抛物线的解析式．
【答案】（1）A(2，2
)，1；（2）﹣1或；（3）①
；②y＝（x﹣1）2+
【解析】
（1）由等边三角形的性质可求点A坐标，由抛物线的性质可求对称轴；
（2）分两种情况讨论，由直角三角形的性质可求点P坐标，代入解析式可求a的值；
（3）①连接AG并延长AG交OB于H，由等边三角形外心的性质可求GH的长，由平行四边形的性质可得GD∥OB，GD＝OQ，由平行线分线段成比例可求GD的长，由勾股定理可求解；
②在OB上截取OM＝BD，连接CM，GM，GB，MD，GD，通过证明△GDE∽△MDC，可得
＝，则当GE最小值为1时，MC最小值为，可得当点C与抛物线顶点P重合，且CM⊥OB时，CM有最小值，即可求点P坐标，代入解析式可求解．
解：（1）如图，连接AG并延长AG交OB于H，
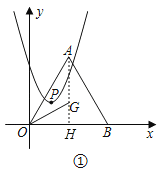
∵点B坐标为（4，0），
∴OB＝4，
∵点G是等边三角形AOB的外心，
∴AH⊥OB，OA＝OB＝4，∠AOB＝60°，
∴∠OAH＝30°，
∴OH＝
OA＝2，AH＝OH＝2，
∴点A（2，2），
∵抛物线y＝ax（x﹣2）+1+＝ax2﹣2ax+1+，
∴对称轴为：直线x＝﹣
＝1；
（2）如图，过点P作PN⊥OB于N，交AO于F，
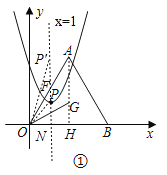
∴ON＝1，
∵点G是等边三角形AOB的外心，
∴OG平分∠AOB，
∴∠AOG＝30°＝∠BOG，
当点P在△AOB内，
∵∠AOG＝2∠AOP，
∴∠AOP＝15°＝∠POG，
∴∠PON＝45°，
∵PN⊥OB，
∴∠PON＝∠OPN＝45°，
∴PN＝ON＝1，
∴点P坐标（1，1），
∴1＝a（1﹣2）+1+，
∴a＝，
当点P在△AOB外，
同理可得∠AOP'＝15°，
∴∠P'ON＝75°，
∴∠OP'N＝15°＝∠AOP'，
∴OF＝P'F，
∵∠AOB＝60°，P'N⊥OB，
∴OF＝2ON＝2＝P'F，FN＝ON＝，
∴P'N＝P'F+FN＝2+，
∴点P坐标为（1，2+），
∴2+＝a（1﹣2）+1+，
∴a＝﹣1，
综上所述：a＝﹣1或；
（3）如图，连接AG并延长AG交OB于H，
∵点G是等边三角形AOB的外心，
∴AG＝2GH，OH＝BH＝2，AH＝2，
∴GH＝
，
∵四边形GDQO为平行四边形，
∴GD∥OB，GD＝OQ，
∴
，
∴GD＝，
∴QH＝
，
∴GQ＝
＝
＝；
②如图，在OB上截取OM＝BD，连接CM，GM，GB，MD，GD，
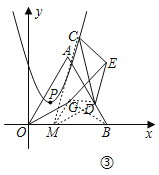
∵点G是等边三角形AOB的外心，
∴OG＝GB，∠GOB＝∠GBO＝∠ABG＝30°，
又∵OM＝BD，
∴△OGM≌△BGD（SAS），
∴MG＝GD，∠OGM＝∠BGD，
∴∠OGB＝∠MGD＝180°﹣30°﹣30°＝120°，
∴MD＝GD，∠GDM＝30°，
∵△CDE中CE＝DE，∠CED＝120°，
∴CD＝DE，∠CDE＝30°，
∴∠MDC＝∠GDE，
，
∴△GDE∽△MDC，
∴＝，
当GE最小值为1时，MC最小值为，
∴当点C与抛物线顶点P重合，且CM⊥OB时，CM有最小值，
∴CM的最小值为顶点P的纵坐标，
∴点P坐标（1，），
∴＝a（1﹣2）+1+，
∴a＝1，
∴抛物线的解析式为：y＝x（x﹣2）+1+＝（x﹣1）2+．
【点题】
考查了二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、等边三角形的性质和垂线段最短等知识，解题关键是添加恰当辅助线构造全等三角形或相似三角形．
