��Ŀ����
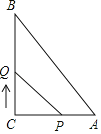
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬AC��6cm��BC��8cm����P�ӵ�A������AC��1cm/s���ٶ����C�ƶ���ͬʱ��Q��C�������CB��2cm/s���ٶ����B�ƶ�����Q�˶���B��ʱ��P��Qֹͣ�˶������P�˶���ʱ��Ϊts��
��1��tΪ��ֵʱ����PCQ���������5cm2��
��2����P��Q���ƶ������У��Ƿ����ijһʱ�̣�ʹ�á�PCQ��������ڡ�ABC�������һ�룿�����ڣ����t��ֵ���������ڣ�˵�����ɣ�
���𰸡���1��1����2�������ڣ����ɼ�����.
��������
��1���ֱ����CP��CQ�ı���ʽ���ٸ����������5�г����̣��ⷽ�̼��ɵó��𰸣�
��2���������������ABC��������ٸ�������PCQ�����������ABC�������һ�����г�һԪ���η��̣������б�ʽ�ж��Ƿ���ʵ���⣬���ɵó���.
�⣺��1��������ã�AP��tcm�� CQ��2tcm����PC����6��t��cm��
��![]() ��2t��6��t����5��
��2t��6��t����5��
��������t2��6t+5��0�����t1��1��t2��5���ᣩ��
��t=1ʱ����PCQ���������5cm2��
��2��������ã�S��ABC��![]() ��ACBC��
��ACBC��![]() ��6��8��24��
��6��8��24��
����![]() ��2t��6��t����
��2t��6��t����![]() ��24��
��24��
�����ģ�t2��6t+12��0��
������62��4��12����12��0���÷�����ʵ���⣬
�����ijһʱ�̣�ʹ����PCQ�����������ABC�������һ�룮

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�