��Ŀ����
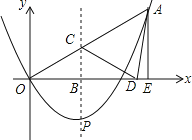
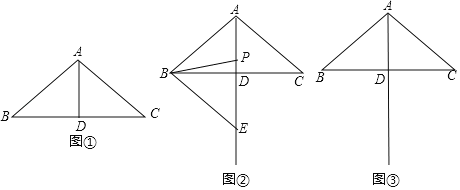
����Ŀ����ͼ�٣��ڡ�ABC�У�AB��AC��3����BAC��100����D��BC���е㣮
С����ͼ�ٽ���������̽�������߶�AD����ȡһ��P������PB�����߶�PB�Ƶ�P����ʱ�뷽����ת80������B�Ķ�Ӧ���ǵ�E������BE���õ���BPE��С�����֣����ŵ�P���߶�AD��λ�õı仯����E��λ��Ҳ�ڱ仯����E������ֱ��AD����࣬Ҳ������ֱ��AD�ϣ���������ֱ��AD���Ҳ࣮
�������С������̽����������������⣺
��1������E��ֱ��AD��ʱ����ͼ����ʾ��
�١�BEP���� ������
������CE��ֱ��CE��ֱ��AB��λ�ù�ϵ���� ����
��2������ͼ���л�����BPE��ʹ��E��ֱ��AD���Ҳ࣬����CE�����ж�ֱ��CE��ֱ��AB��λ�ù�ϵ����˵�����ɣ�
��3������P���߶�AD���˶�ʱ����AE����Сֵ��
���𰸡���1����50�㣻��AB��EC����2�������������3��3.
��������
��1���ٸ��ݡ�BPE=80�㣬PB=PE��������𰸣��ڸ��ݡ�AB��AC����BAC��100�㡱�����Եõ�AE��ֱƽ���߶�BC���Ӷ��õ�EB��EC�������õ���ECB����EBC������֤�á�ABC����ECB���Ӷ��õ��𰸣�
��2����PΪԲ�ģ�PBΪ�뾶����P���õ�PB��PC���ٸ���ͬ�����Ե�Բ�ܽ���Բ�ĵ�һ�������BCE�Ķ����Ӷ��õ��𰸣�
��3����AH��CE��H����E������CE���˶�����P���߶�AD���˶�������P�˶������A�غ�ʱ��AEȡ��Сֵ���ʶ��õ���.
�⣺��1������ͼ���У�

�ߡ�BPE��80�㣬PB��PE��
���PEB����PBE��50�㣬
�ڽ��ۣ�AB��EC��
���ɣ���AB��AC��BD��DC��
��AD��BC��
���BDE��90�㣬
���EBD��90�㩁50�㣽40�㣬
��AE��ֱƽ���߶�BC��
��EB��EC��
���ECB����EBC��40�㣬
��AB��AC����BAC��100�㣬
���ABC����ACB��40�㣬
���ABC����ECB��
��AB��EC��
�ʴ�Ϊ50��AB��EC��
��2����ͼ���У���PΪԲ�ģ�PBΪ�뾶����P��
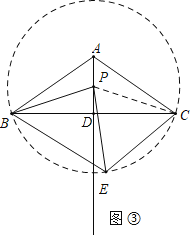
��AD��ֱƽ���߶�BC��
��PB��PC��
���BCE��![]() ��BPE��40�㣬
��BPE��40�㣬
�ߡ�ABC��40�㣬
��AB��EC��
��3����ͼ���У���AH��CE��H��
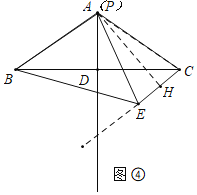
�ߵ�E������CE���˶�����P���߶�AD���˶���
�൱��P�˶������A�غ�ʱ��AE��ֵ��С����ʱAE����Сֵ��AB��3��

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�����Ŀ�������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μӱ����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ƽ���ɼ� | ��λ�� | |
�� | 10 | 8 | 9 | 8 | 10 | 9 | 9 | �� |
�� | 10 | 7 | 10 | 10 | 9 | 8 | �� | 9.5 |
��1����ɱ�����բ��� �������� ����
��2�����������β��Գɼ��ķ��
��3���������β��Գɼ�����Ϊ![]() ������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�