题目内容
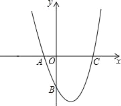
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ,抛物线的对称轴是 x=3;
,抛物线的对称轴是 x=3;
(2)存在;P点坐标为(3,![]() ).
).
(3)在直线AC下方的抛物线上存在点N,使△NAC面积最大.N(![]() ,-3)
,-3)
【解析】
(1)根据已知条件可设抛物线的解析式为y=a(x-1)(x-5).
把点A(0,4)代入上式,解得a=![]() .
.
∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() .
.
∴抛物线的对称轴是x=3.
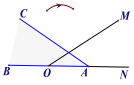
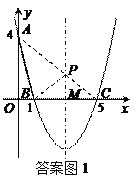
(2)存在,P点的坐标是(3,![]() ).如图1,连接AC交对称轴于点P,连接BP,AB.
).如图1,连接AC交对称轴于点P,连接BP,AB.
∵点B与点C关于对称轴对称,
∴PB=PC.
∴AB+AP+PB=AB+AP+PC=AB+AC.
∴此时△PAB的周长最小.
设直线AC的解析式为y=kx+b.把A(0,4),C(5,0)代入y=kx+b,得
![]() 解得
解得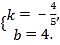
∴y=-![]() x+4.
x+4.
∵点P的横坐标为3,
∴y=-![]() ×3+4=
×3+4=![]() .
.
∴P(3,![]() ).
).
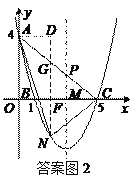
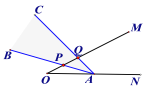
(3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大.
如图2,设N点的横坐标为tt,此时点N(t,![]() t2-
t2-![]() t+4)(0<t<5).
t+4)(0<t<5).
过点N作y轴的平行线,分别交x轴,AC于点F,G,过点A作AD⊥NG,垂足为D.
由(2)可知直线AC的解析式为y=-![]() x+4.
x+4.
把x=t代入y=-![]() x+4,得y=-
x+4,得y=-![]() t+4.
t+4.
∴G(t,-![]() t+4).
t+4).
∴NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t.
t2+4t.
∵AD+CF=OC=5,
∴S△NAC=S△ANG+S△CGN=![]() NG·AD+
NG·AD+![]() NG·CF=
NG·CF=![]() NG·OC
NG·OC
=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() .
.
∵当t=![]() 时,△NAC面积的最大值为
时,△NAC面积的最大值为![]() .
.
由t=![]() ,得y=
,得y=![]() ×(
×(![]() )2-
)2-![]() ×
×![]() +4=-3.
+4=-3.
∴N(![]() ,-3).
,-3).

【题目】如图所示的是丽水市统计局公布的2010~2013年全社会用电量的折线统计图.
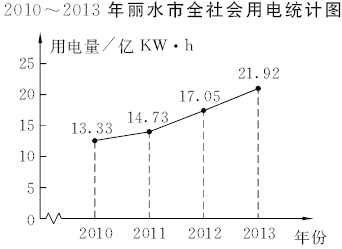
(1)根据统计图填写统计表:
2010~2013年丽水市全社会用电量统计表
年份 | 2010 | 2011 | 2012 | 2013 |
全社会用电量 (单位:亿KW·h) | 13.33 |
(2)根据丽水市2010年至2013年全社会用电量统计数据,求2011~2013年全社会用电量的年平均增长率(保留到0.01).