题目内容
【题目】如图,已知抛物线y=(x﹣1)2+k的图象与x轴交于点A(﹣1,0),C两点,与y轴交于点B.
(1)求抛物线解析式及B点坐标;
(2)在抛物线上是否存在点P使S△PAC=![]() S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形,若存在,求出Q点坐标,若不存在,请说明理由.

【答案】(1) y=x2﹣2x﹣3,点B坐标为(0,﹣3);(2)见解析;(3)见解析.
【解析】
(1)把A(-1,0)代入抛物线y=(x﹣1)2+k,求出k即可解决问题.(2)存在.先求出△ABC的面积,再根据已知条件求出点P的纵坐标,利用待定系数法即可解决问题.(3)存在.分三种情形讨①当AQ=AB时,有两种情形a、当![]() 在x轴上方,;b、当
在x轴上方,;b、当![]() 在x轴下方时,利用勾股定理即可解决问题.②当BA=BQ时,此时Q在x轴上,即
在x轴下方时,利用勾股定理即可解决问题.②当BA=BQ时,此时Q在x轴上,即![]() (1,0)③当QA=QB时,点Q在AB的垂直平分线上,求出线段AB的垂直平分线的解析式即可解决问题.
(1,0)③当QA=QB时,点Q在AB的垂直平分线上,求出线段AB的垂直平分线的解析式即可解决问题.
(1)把A(﹣1,0)代入抛物线y=(x﹣1)2+k得,0=4+k,
∴k=﹣4,
∴抛物线解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3,
令x=0,得y=﹣3,
∴点B坐标为(0,﹣3).
(2)存在.如图1中,
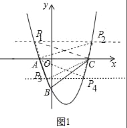
理由:令y=0,则x2﹣2x﹣3=0,
∴x=﹣1或3,
∴点A(﹣1,0),C(3,0),
∴S△ABC=![]() ×4×3=6,
×4×3=6,
∵S△PAC=![]() S△ABC,
S△ABC,
∴S△PAC=![]() ,设P(m,n),
,设P(m,n),
则有![]() ×4×|n|=
×4×|n|=![]() ,
,
∴n=![]() ,
,
当n=![]() 时,m2﹣2m﹣3=
时,m2﹣2m﹣3=![]() ,解得m=﹣
,解得m=﹣![]() 或
或![]() ,此时P(﹣
,此时P(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
当n=﹣![]() 时,m2﹣2m﹣3=﹣
时,m2﹣2m﹣3=﹣![]() ,解得m=
,解得m=![]() 或
或![]() ,此时P(
,此时P(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
综上所述,满足条件的P点坐标为(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
(3)如图2中,存在.

①当AQ=AB时,有两种情形a、当Q1在x轴上方,此时Q1(1,![]() );b、当Q2在x轴下方时,此时Q2(1,﹣
);b、当Q2在x轴下方时,此时Q2(1,﹣![]() ).
).
②当BA=BQ时,此时Q在x轴上,Q3(1,0).
③当QA=QB时,点Q在AB的垂直平分线上,
∵A(﹣1,0),B(0,﹣3),
∴直线AB解析式为y=﹣3x﹣3,线段AB的中点为(﹣![]() ,﹣
,﹣![]() ),
),
设线段AB的中垂线的解析式为y=![]() x+m.
x+m.
∴﹣![]() =﹣
=﹣![]() +m,
+m,
∴m=﹣![]() ,
,
∴线段AB的中垂线的解析式为y=![]() x﹣
x﹣![]() ,与对称轴的交点Q4(1,﹣1),
,与对称轴的交点Q4(1,﹣1),
综上所述,满足条件的点Q坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() )或(1,0)或(1,﹣1).
)或(1,0)或(1,﹣1).