Question

【题目】如图，是等边三角形，是角平分线，过点作于，交边的延长线于点，.

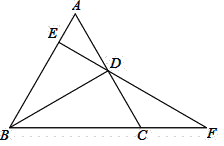
(1)求证：是等腰三角形；

(2)求的长.

Answer 1

【答案】（1）证明见详解；（2）12

【解析】

(1)根据已知条件得∠ADE=30°,即∠CDF=30°,由外角定理得∠ACB=∠CDF+∠F,得∠F=30°,进而得到CD=CF,得出结论；

(2) 由于，∠ADE=30°,AE=2,可得AD=4,进而可得AC和CD的长，由BC=AC,CD=CF,可得BF的长度.

(1)∵是等边三角形，是角平分线，

∴∠A=∠ACB=60°,AC=BC,AD=CD=AC,

∵于，

∴∠ADE=90°-∠A=30°,

∴∠CDF=30°,

又∵∠ACB=60°, ∠ACB=∠CDF+∠F,

∴∠F=30°,

∴∠CDF+∠F=30°,

∴CD=CF,

∴是等腰三角形.

(2) ∵于，∠ADE=30°,AE=2,

∴AD=2AE=4,

∴CD=CF=4,AC=2AD=8,

∵是等边三角形，

∴BC=AC=8,

∴BF=BC+CF=8+4=12.