Question

【题目】如图，抛物线y＝ax2﹣2ax+m的图象经过点P（4，5），与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，且S△PAB＝10．

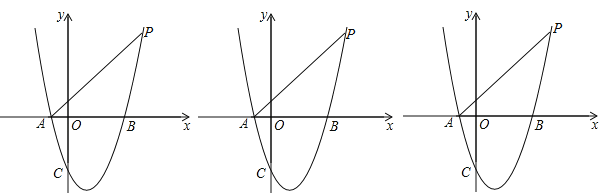
（1）求抛物线的解析式；

（2）在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等？若存在，求出Q点的坐标，若不存在，请说明理由；

（3）过A、P、C三点的圆与抛物线交于另一点D，求出D点坐标及四边形PACD的周长．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）点Q的坐标为：（﹣2，5）或（﹣，﹣）；（3）6+4．

【解析】

（1）因为抛物线y＝ax2﹣2ax+m，函数的对称轴为：x＝1，S△PAB＝10＝×AB×yP＝AB×5，解得AB=4，即可求解；（2）分A、B在点Q（Q′）的同侧；点A、B在点Q的两侧两种情况，分别求解即可；（3）过点P作PO′⊥x轴于点O′，则点O′（4，0），则AO′＝PO′＝5，而CO′＝5，故圆O′是过A、P、C三点的圆，即可求解．

解：

（1）y＝ax2﹣2ax+m，函数的对称轴为：x＝1，

S△PAB＝10＝×AB×yP＝AB×5，解得：AB＝4，

故点A、B的坐标分别为：（﹣1，0）、（3，0），

抛物线的表达式为：y＝a（x+1）（x﹣3），

将点P的坐标代入上式并解得：a＝1，

故抛物线的表达式为：y＝x2﹣2x﹣3…①；

（2）①当A、B在点Q（Q′）的同侧时，如图1，

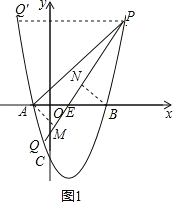
△PAQ′和△PBQ′的面积相等，则点P、Q′关于对称轴对称，

故点Q′（﹣2，5）；

②当A、B在点Q的两侧时，如图1，

设PQ交x轴于点E，分别过点A、B作PQ的垂线交于点M、N，

△PAQ和△PBQ的面积相等，则AM＝BN，

而∠BEN＝∠AEM，∠AME＝∠BNE＝90°，

∴△AME≌△BNE（AAS），

∴AE＝BE，

即点E是AB的中点，则点E（1，0），

将点P、E的坐标代入一次函数表达式并解得：

直线PQ的表达式为：y＝x﹣…②，

联立①②并解得：x＝﹣或4（舍去4），

故点Q（﹣，﹣），

综上，点Q的坐标为：（﹣2，5）或（﹣，﹣）；

（3）过点P作PO′⊥x轴于点O′，则点O′（4，0），则AO′＝PO′＝5，而CO′＝5，

故圆O′是过A、P、C三点的圆，

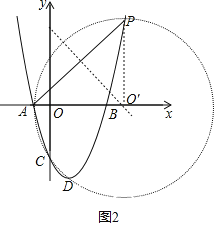
设点D（m，m2﹣2m﹣3），点O′（4，0），则DO′＝5，

即（m﹣4）2+（m2﹣2m﹣3）2＝25，

化简得：m（m+1）（m﹣1）（m﹣4）＝0，

解得：m＝0或﹣1或1或4（舍去0，﹣1，4），

故：m＝1，

故点D（1，﹣4）；

四边形PACD的周长＝PA+AC+CD+PD＝．