题目内容
【题目】在菱形ABCD中，∠BAD＝α，E为对角线AC上的一点（不与A，C重合）将射线EB绕点E顺时针旋转β角之后，所得射线与直线AD交于F点．试探究线段EB与EF的数量关系．
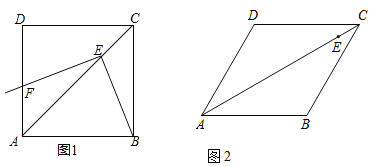
（1）如图1，当α＝β＝90°时，EB与EF的数量关系为 ；
（2）如图2，当α＝60°，β＝120°时，
①依题意补全图形；
②探究（1）的结论是否成立，若成立，请给出证明；若不成立，请举出反例证明．
【答案】（1）EB＝EF；（2）①见解析；②成立，理由见解析
【解析】
（1）作EM⊥AD于M，EN⊥AB于N．根据角平分线的性质可证EM=EN，从而根据“ASA”可证△EMF≌△ENB，由全等三角形对应边相等得到EB=EF；
（2）①依题意以E为旋转中心，在EB顺时针方向作∠BEF=120°，与AD的延长线交于F.
②方法一：过点E作EM⊥AF于M，EN⊥AB于N，利用菱形的性质得出，∠DAC=∠BAC，再用角平分线的性质，得出EM=EN，进而证明△EFM≌△EBN即可证明EF=EB；
方法二：连接ED，利用菱形的性质可证明△AED≌△AEB，所以ED=EB，∠ADE=∠ABE，再证明∠F=∠FDE，根据等角对等边EF=ED，即可证明EF=EB.
（1）EB＝EF，
理由是：如图1，作EM⊥AD于M，EN⊥AB于N．
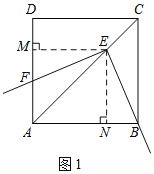
∵四边形ABCD是菱形，且∠BAD＝90°，
∴菱形ABCD是正方形，
∴AE平分∠DAB，
∴EM＝EN，
∵∠BEF＝∠NEM＝90°，
∴∠MEF＝∠NEB，
∵∠EMF＝∠BNE＝90°，
∴△EMF≌△ENB（ASA），
∴EB＝EF；
故答案为：EB＝EF；
（2）①补全图形如图2所示，
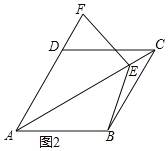
②结论依然成立EB＝EF；
证法1：如图3，
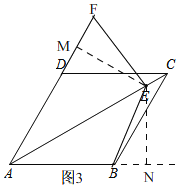
过点E作EM⊥AF于M，EN⊥AB于N．
∵四边形ABCD为菱形，
∴∠CAD＝∠CAB．
∵EM⊥AF，EN⊥AB．
∴∠FME＝∠ENB＝90°，EM＝EN，
∵∠BAD＝60°，∠BEF＝120°，
∴∠F+∠ABE＝360°﹣∠BAD﹣∠BEF＝180°．
∵∠ABE+∠EBN＝180°，
∴∠F＝∠EBN；
在△EFM与△EBN中，
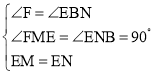
∴△EFM≌△EBN（AAS）．
∴EF＝EB；
证法2：如图4，连接ED
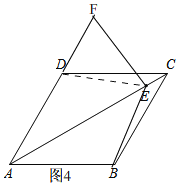
∵四边形ABCD是菱形，
∴AD＝AB，∠DAC＝∠BAE．
又∵AE＝AE，
∴△ADE≌△ABE（SAS）．
∴ED＝EB，∠ADE＝∠ABE，
又∵∠DAB＝60°，∠BEF＝120°．
∴∠F+∠ABE＝180°．
又∵∠ADE+∠FDE＝180°，
∴∠F＝∠FDE．
∴EF＝ED．
∴EF＝EB．
