Question

【题目】在平面直角坐标系xOy中，点A为平面内一点，给出如下定义：过点A作AB⊥y轴于点B，作正方形ABCD（点A，B，C，D顺时针排列），即称正方形ABCD为以A为圆心，OA为半径的⊙A的“友好正方形”．
（1）如图1，若点A的坐标为（1，1），则⊙A的半径为 ．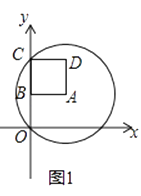
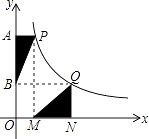
（2）如图2，点A在双曲线y= （x＞0）上，它的横坐标是2，正方形ABCD是⊙A的“友好正方形”，试判断点C与⊙A的位置关系，并说明理由．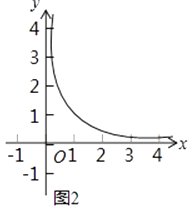
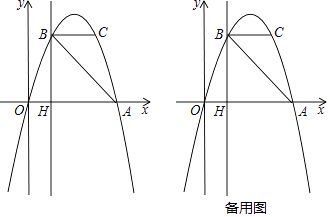
（3）如图3，若点A是直线y=﹣x+2上一动点，正方形ABCD为⊙A的“友好正方形”，且正方形ABCD在⊙A的内部时，请直接写出点A的横坐标m的取值范围．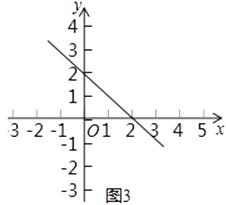

Answer 1

【答案】
（1）
（2）解：如图2中，

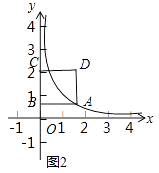
∵A（2， ），∴O A=

∵AC=2 = =

∴O A＜A C，

∴点C在⊙A外．

（或如图，利用勾股定理直观分析：∵OB＜BC，AB=AB，∴O A＜A C也可以）

（3）解：如图3中，

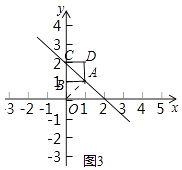
∵点A是直线y=﹣x+2上一动点，直线与坐标轴是夹角为45°，

又∵四边形ABCD是正方形，

∴点C（0，2），

∴当AC＜OA时，正方形ABCD在⊙A内部，

∵AC=OA时，点A（1，1），

∴m＜1时，AC＜OA，

∵m=0时，正方形不存在，

∴m＜1且m≠0时，正方形ABCD在⊙A内部

【解析】解：（1）如图1中，连接OA．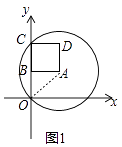
∵A（1，1），AB⊥y轴，
∴AB=OB=1，∠ABO=90°，
∴OA= = = ，
∴⊙A的半径为 ．
所以答案是 ；