题目内容
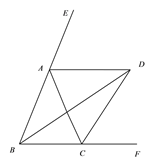
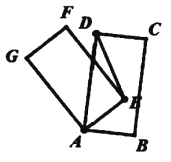
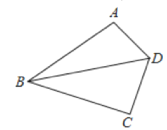
【题目】四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=120°,求证:BD=AD+CD.
【答案】见解析.
【解析】
首先延长AD到E,使DE=DC,连接CE,由∠ADC=120°,可得∠1=60°,再有DE=DC可根据有一个角是60°的等腰三角形是等边角形证出△DEC是等边三角形,同理证出△ABC也是等边三角形,根据等边三角形的性质可得:AB=CB,DC=CE,∠3=∠4=60°,进而得到∠BCD=∠ACE,再证明△BCD≌△ACE,得出BD=AE,由AE=AD+DE,DE=DC进行等量代换可得BD=AD+CD.
证明:延长AD到E,使DE=DC,连接CE,
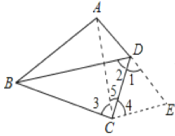
∵∠ADC=120°,
∴∠1=180°120°=60°,
∵DC=DE,
∴△DEC是等边三角形(有一个角是60°的等腰三角形是等边角形),
∴DC=CE,∠4=60°,
∵∠ABC=60°,AB=CB,
∴△ABC是等边三角形(有一个角是60°的等腰三角形是等边角形),
∴AC=CB,∠3=60°,
∴∠3=∠4=60°,
∴∠3+∠5=∠4+∠5,
即:∠BCD=∠ACE,
∵在△BCD和△ACE中:
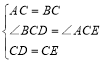 ,
,
∴△BCD≌△ACE(SAS),
∴BD=AE(全等三角形对应边相等),
∵AE=AD+DE=AD+DC,
∴DB=AD+DC.

【题目】某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 39.5﹣49.5 | 2 | 0.05 |
2 | 49.5﹣59.5 | 4 | 0.10 |
3 | 59.5~69.5 | a | 0.20 |
4 | 69.5~79.5 | 10 | 0.25 |
5 | 79.5﹣89.5 | b | c |
6 | 89.5﹣100 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
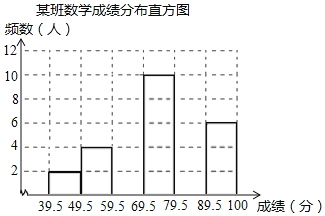
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?