题目内容
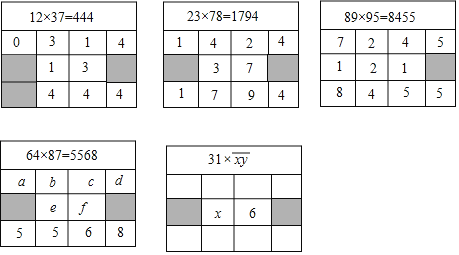
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
【答案】(1)5;(2)10或-12;(3)7,![]()
【解析】
(1)设绝对值符号里左边的数为a,根据a>0时,(6-a)-2=-|a+1|+5;a<0时,(a+8)-2=-|a+1|+5的规律即可求解;
(2)由a>0时,(6-a)-2=-|a+1|+5;a<0时,(a+8)-2=-|a+1|+5的规律,分情况讨论即可求解;
(3)设绝对值符号里左边的数为a,由题意得![]() ,然后根据非负数的性质即可求解.
,然后根据非负数的性质即可求解.
解:(1)设绝对值符号里左边的数为a,由题意可得:a>0时,(6-a)-2=-|a+1|+5;a<0时,(a+8)-2=-|a+1|+5
∵1>0
∴6-a=1
解得:a=5;
故答案为:5
(2)由(1)可知:
当x>0时x=6-(-4)=10
当x<0时,x=-4-8=-12
故答案为:10或-12;
(3)设绝对值符号里左边的数为a. 由题意,得![]() .
.
所以![]() .
.
因为![]() 的最小值为0,所以
的最小值为0,所以![]() 的最小值为0.所以y的最大值为7.
的最小值为0.所以y的最大值为7.
此时![]() =0.所以
=0.所以![]() .
.
所以此时等式为![]() .
.
答:y的最大值为7,此时等式为![]() .
.

练习册系列答案
相关题目