题目内容
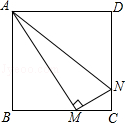
如图,在△ABC中,∠BAC=90°, BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.

(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)y=-x2+2x+3;(2)P1(1,4) P2(1,-2)  .
.
 .
.试题分析:(1)根据题意知点B的坐标为(0,3)抛物线的对称轴方程为x=1,所以A点坐标为(1,4),C点坐标为(2,3),由此可求抛物线的解析式.
(2)分两种情况:CD为直角边,CD为斜边进行讨论,由勾股定理得到方程即可求出P点坐标.
试题解析:(1)∵y=ax2-2ax+3
∴它的对称轴为直线x=

令x=0,则y=3,
∴B(0,3)
根据抛物线的对称性知:C(2,3),A(1,4)
把A(1,4)代入y=ax2-2ax+3,得:a=-1
∴抛物线的解析式为:y=-x2+2x+3;
(2)存在.分两种情况:
(1)当CD为直角边时,设P(1,a):
i)当点P在x轴上方时,DP=
 ,CP=
,CP= ,
, ,
,∵CD2+CA2=AD2
∴18+2=4+a2
即:a2=16
解得a=±4(负舍去)
∴a=4
ii)当点P在x轴下方时,CD2+DP2=CP2
∴

解得:a=-2
(2)当CD为斜边时,同理可以得出:a=

综上所述,点P的坐标分别为:P1(1,4) P2(1,-2)


练习册系列答案
相关题目
 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 . 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
. ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
. ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: 中,点
中,点 ,
, 的“面积坐标”为
的“面积坐标”为 ,
, 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;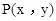 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.

 ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
 B.
B. C.
C. D.
D.
 的顶点坐标为 .
的顶点坐标为 .