��Ŀ����
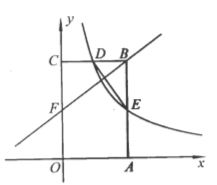
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�Ķ���A��C�����������ϣ���OA=4��OC=3������M�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���AO���յ�O�ƶ�������N�ӵ�C������CB���յ�B��ͬ�����ٶ��ƶ��������������˶���x�루0��x��4��ʱ������N��NP��BC�ڵ�P������MP��

��1��ֱ��д����B�����꣬�������P�����꣨�ú�x��ʽ�ӱ�ʾ����
��2�����OMP�����ΪS����S��x֮��ĺ�������ʽ����xΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3�������������˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ��OMP�ǵ��������Σ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��B������Ϊ��4��3������P������Ϊ��x��![]() x������2����x=2ʱ��S�����ֵ�����ֵΪ
x������2����x=2ʱ��S�����ֵ�����ֵΪ![]() ��(3) M������Ϊ��
��(3) M��������![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����
��������
�����������1�����ݾ���OABC��OA=4��OC=3�Լ����ε����ʣ��ó�B�����꣬����PG��AB���ó���OPG�ס�OBA���������������ζ�Ӧ�߳ɱ����ó�P�����ꣻ
��2������PG�Լ�OM�ij���ʾ����OMP��������ٸ��ݶ��κ���������������ֵ���ɣ�
��3����OMP�ǵ���������ʱ���������������PO=PM����OP=OM����OM=PM������ͼ�Σ��ֱ�������ɣ�
�����������1���߾���OABC�У�OA=4��OC=3��
��B��������4��3����
��ͼ���ӳ�NP����OA�ڵ�G����PG��AB��OG=CN=x��

��PG��AB��
���OPG�ס�OBA��
��![]() ����
����![]() �����PG=
�����PG=![]() x��
x��
���P��������x��![]() x����
x����
��2�����ڡ�OMP�У�OM=4-x��OM���ϵĸ�Ϊ![]() x��
x��
��S=![]() ��4-x��
��4-x��![]() x=-
x=-![]() x2+
x2+![]() x��
x��
��S��x֮��ĺ�������ʽΪS=-![]() x2+
x2+![]() x��0��x��4����
x��0��x��4����
�䷽����S=-![]() ��x-2��2+
��x-2��2+![]() ��
��
�൱x=2ʱ��S�����ֵ�����ֵΪ![]() ��
��
��3������ijһʱ�̣�ʹ��OMP�ǵ��������Σ��������£�
���籸��ͼ1��
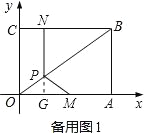
��PO=PM����OG=GM=CN=x��
��3x=4����ã�x=![]() ��
��
����M��![]() ��0����
��0����
���籸��ͼ2��

��OP=OM����![]() =OM��
=OM��
��![]() x=4-x����ã�x=
x=4-x����ã�x=![]() ��
��
����M��![]() ��0����
��0����
���籸��ͼ3��
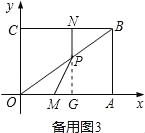
��OM=PMʱ��
��PG=![]() x��GM=OM-OG=��4-x��-x=4-2x��
x��GM=OM-OG=��4-x��-x=4-2x��
��PM2=PG2+GM2=��![]() x��2+��4-2x��2��
x��2+��4-2x��2��
��OM=4-x��
�ࣨ4-x��2=��![]() x��2+��4-2x��2����ã�x=
x��2+��4-2x��2����ã�x=![]() ��
��
���ԣ�M��![]() ��0����
��0����
����������M��������![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����