题目内容
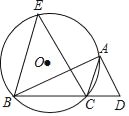
【题目】如图，点B，C为⊙O上一动点，过点B作BE∥AC，交⊙O于点E，点D为射线BC上一动点，且AC平分∠BAD，连接CE．
（1）求证：AD∥EC；
（2）连接EA，若BC=6，则当CD= 时，四边形EBCA是矩形．
【答案】（1）见解析；（2）6
【解析】
（1）欲证明AD∥EC，只要证明∠ACE=∠DAC即可；
（2）当四边形ACBE是矩形时，∠ACB=90°，根据等腰三角形的性质即可解决问题；
（1）证明：∵AC平分∠BAD，
∴∠BAC=∠DAC，
∵∠E=∠BAC，
∴∠E=∠DAC
∵BE∥AC，
∴∠E=∠ACE，
∴∠ACE=∠DAC，
∴AD∥EC．
（2）当四边形ACBE是矩形时，∠ACB=90°，
∴∠ACB=∠ACD=90°，
∵∠BAC=∠DAC，
∴∠ABD=∠D，
∴AB=AD，
∴BC=CD=6，
故答案为6．
练习册系列答案
相关题目
【题目】数学老师在一次“探究性学习”课中，设计了如下数表：
| 2 | 3 | 4 | 5 | … |
| 3 | 8 | 15 | 24 | … |
| 4 | 6 | 8 | 10 | … |
| 5 | 10 | 17 | 26 | … |
由表可知，当
时，
，
，
；
当
时，
，
，
；
………
（1）当
时，
________，
_________，
________.
（2）请你分别观察
，
，
与
之间的关系，并分别用含有
的代数式表示 ，，.
________，_________，________.
（3）猜想以，，为边的三角形是否为直角三角形，并说明理由.
