题目内容
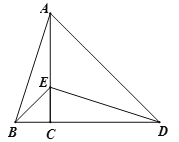
【题目】当a取什么整数时,方程![]() +
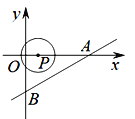
+![]() +
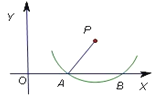
+![]() =0只有一个实根,并求此实根.
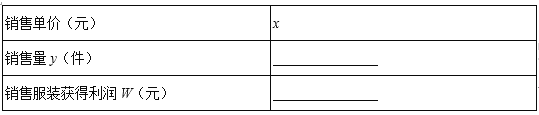
=0只有一个实根,并求此实根.
【答案】a=﹣4时,原方程恰有一个实根x=1;a=﹣8时,原方程恰有一个实根x=﹣1
【解析】
先将原方程化为![]() =0,再分三种情况进行讨论:
=0,再分三种情况进行讨论:
(1)若x≠0且x≠2,则2x2﹣2x+4+a=0,由原分式方程恰有一个实根,得出△=(﹣2)2﹣4×2×(4+a)=﹣28﹣8a=0,依此求出a的值;
(2)若方程2x2﹣2x+4+a=0,有一个根为x=0,代入求出a=﹣4,再解方程即可;
(3)若方程2x2﹣2x+4+a=0,有一个根为x=2,代入求出a=﹣8,再解方程即可.
解:原方程化为![]() =0.
=0.
(1)若x≠0且x≠2,则2x2﹣2x+4+a=0,
∵原分式方程恰有一个实根,
∴△=0,即△=(﹣2)2﹣4×2×(4+a)=﹣28﹣8a=0,
则a=﹣![]() ,
,
于是x1=x2=![]() ,
,
但a取整数,则舍去;
(2)若方程2x2﹣2x+4+a=0,有一个根为x=0,则a=﹣4,
这时原方程为![]() ,
,
去分母得2x2﹣2x=0,
解得x=0,x=1,
显然x=0是增根,x=1是原分式方程的根;
(3)若方程2x2﹣2x+4+a=0,有一个根为x=2,则a=﹣8,
这时,原方程为![]()
去分母,得2x2﹣2x﹣4=0,
解得x=2,x=﹣1,
显然x=2是增根,x=﹣1是原分式方程的根;
经检验当a=﹣4时,原方程恰有一个实根x=1;当a=﹣8时,原方程恰有一个实根x=﹣1.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目