��Ŀ����
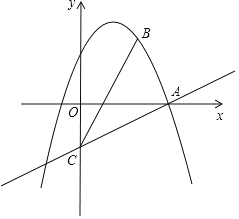
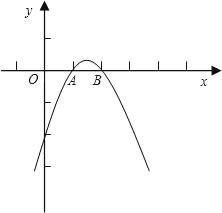
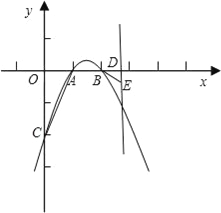
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��a��0����ͼ����A��1��0����B��2��0����C��0����2����ֱ��x��m��m��2����x�ύ�ڵ�D��
��1������κ����Ľ���ʽ��
��2����ֱ��x��m��m��2������һ��E����E�ڵ������ޣ���ʹ��E��D��BΪ���������������A��O��CΪ��������������ƣ���E�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£����������Ƿ����һ��F��ʹ���ı���ABEFΪƽ���ı��Σ������ڣ������F������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ��2��
��2��![]() ��3�����ڣ�
��3�����ڣ�![]()
��������
����
��1����֪�����߾��������㣬����������ߵĽ���ʽΪһ��ʽ![]() ���ٽ��������������뵽һ��ʽ�У��õ���Ԫһ�η����鼴����⣻
���ٽ��������������뵽һ��ʽ�У��õ���Ԫһ�η����鼴����⣻
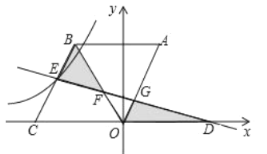
��2����AOC����BDE����ֱ�������Σ���ֱ���⣬�����Ķ�Ӧ��ϵ��ȷ��������Ӧ���������ۣ������������εĶ�Ӧ�߳ɱ������E���������
��3��A��B������ȷ���ĵ㣬E��������к���mҲ�ɿ�����ȷ���ĵ㣬��ɸ����������������ȷ�����ĸ���F�����꣬����F���������ϣ���F���������뵽�������еõ�����m�ķ��̣���������F������.
�⣺��1������A��1��0����B��2��0����C��0����2��������κ���y=ax2+bx+c�У���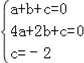
���a=��1��b=3��c=��2��
��y=��x2+3x��2����2�֣�
��2����AO=1��CO=2��BD=m��2��
����EDB�ס�AOCʱ����![]() =
=![]() ��
��
��![]() =
=![]() �����ED=
�����ED=![]() ��
��
�ߵ�E�ڵ������ޣ�
��E1��m��![]() ����
����
����BDE�ס�AOCʱ��![]() =
=![]() ʱ����
ʱ����![]() =
=![]() ��
��
���ED=2m��4��
�ߵ�E�ڵ������ޣ�
��E2��m��4��2m����
������E1��m��![]() ����E2��m��4��2m��.
����E2��m��4��2m��.
��3�������������ϴ���һ��F��ʹ���ı���ABEFΪƽ���ı��Σ���
EF=AB=1����F�ĺ�����Ϊm��1��
����E1������Ϊ��m��![]() ��ʱ����F1������Ϊ��m��1��
��ʱ����F1������Ϊ��m��1��![]() ����
����
�ߵ�F1�������ߵ�ͼ���ϣ�
��![]() =����m��1��2+3��m��1����2��
=����m��1��2+3��m��1����2��
��2m2��11m+14=0��
����2m��7����m��2��=0��
��m=![]() ��m=2����ȥ����
��m=2����ȥ����
��F1��![]() ����
����![]() ����
����
����E2������Ϊ��m��4��2m��ʱ����F2������Ϊ��m��1��4��2m����
�ߵ�F2�������ߵ�ͼ���ϣ�
��4��2m=����m��1��2+3��m��1����2��
��m2��7m+10=0��
����m��2����m��5��=0����m=2����ȥ����m=5��
��F2��4����6����
����F1��![]() ����
����![]() ����F2��4����6����
����F2��4����6����