题目内容
【题目】如图,等腰三角形ABC中,AB=AC.
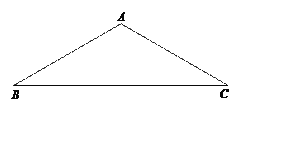
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30°,求证:AB与(1)中所作⊙O相切.
【答案】(1)作图作法见解析;(2)证明见解析.
【解析】分析:(1)①作AC的垂直平分线交BC于点O,以点O为圆心,OC为半径作⊙O,则⊙O为所求作的圆;
(2)连接OA,由等腰三角形的性质可求∠BAC=120°,∠OAC=∠C=30°,从而求得∠BAO=90°,由切线的判定方法可知AB与(1)中所作⊙O相切.
详解:(1)作法:
①作AC的垂直平分线交BC于点O
②以点O为圆心,OC为半径作⊙O,则⊙O为所求作的圆

(2)连接OC,∵AB=AC,
∴∠C=∠B=30°,
∴∠BAC=120°,∵OA=OC,
∴∠OAC=∠C=30°,
∴∠BAO=90°,
∵点A在⊙O上,
∴AB与⊙O相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目