题目内容
【题目】已知矩形AOBC的边AO、OB分别在y轴、x轴正半轴上,点C的坐标为(8,6),点E是x轴上任意一点,连接EC,交AB所在直线于点F,当△ACF为等腰三角形时,EF的长为_____.
【答案】5或![]() 或
或![]() .
.
【解析】
△ACF是等腰三角形,需要分三种情况进行讨论求解.
解:△ACF为等腰三角形有三种情况:
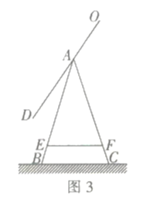
①如图①,当AF=CF时,点E与点O重合,
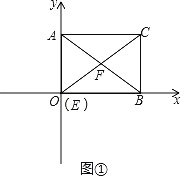
由题意得OB=8,BC=6,
∴由勾股定理得OC=10,
∵四边形AOBC为矩形,
∴EF=5;
②如图②,当AF=AC=8时,
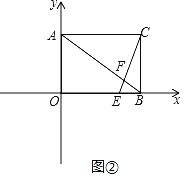
由①可知OC=10,
∵四边形AOBC为矩形,
∴AB=OC=10,AC∥OB,
∴△AFC∽△BFE,
∴![]() =
=![]() =
=![]() ,
,
∴BE=BF=10﹣8=2,
∴在Rt△BCE中,由勾股定理得:CE=![]() =
=![]() ,
,
∴![]() =
=![]() =4,
=4,
∴EF=![]() CE=
CE=![]() ;
;
③如图③,当CF=AC=8时,过点C作CD⊥AF于点D,
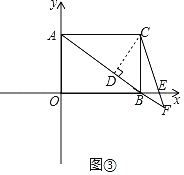
∴AD=DF,
∵AC=8,BC=6,AB=10,
∴CD=![]() =
=![]() ,
,
∴在Rt△ACD中,由勾股定理得:AD=![]() =
=![]() ,
,
∴BD=AB﹣AD=10﹣![]() =
=![]() ,DF=AD=
,DF=AD=![]() ,AF=
,AF=![]() ,BF=DF﹣BD=
,BF=DF﹣BD=![]() ,
,
∵AC∥OE,
∴△AFC∽△BFE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=![]() ,
,
∵CF=AC,
∴EF=BE,
∴EF=![]() .
.
综上所述,EF的长为5或![]() 或
或![]() .
.
故答案为:5或![]() 或
或![]() .
.

练习册系列答案
相关题目